题目内容
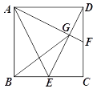
【题目】如图，已知四点A、B、C、D．
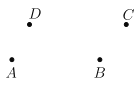
（1）用圆规和无刻度的直尺按下列要求与步骤画出图形：
①画直线AB．
②画射线DC．
③延长线段DA至点E，使
．(保留作图痕迹)
④画一点P，使点P既在直线AB上，又在线段CE上．
（2）在（1）中所画图形中，若
cm，
cm，点F为线段DE的中点，求AF的长．
【答案】（1）见解析；（2）0.5cm．
【解析】
(1)①画直线AB，直线向两边无限延伸；②画射线DC，D为端点，再沿CD方向延长；③画线段DA和AE，线段不能向两方无限延伸；④画线段CE，与直线AB相交于P；（2）利用线段之间的关系解答即可；
解：
（1）如图，该图为所求，
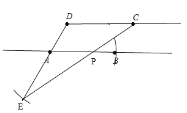
(2)∵AB=2cm，AB=AE，
∴AE=2cm，AD=1cm，
∵点F为DE的中点，
∴EF=
DE=
cm，
∴AF=AE-EF=2-=cm；
∴AF=0.5cm.
练习册系列答案
相关题目
【题目】如图，是一种斜挎包，其挎带由双层部分、单层部分和调节扣构成．乐乐用后发现，通过调节扣加长或缩短单层部分的长度，可以使挎带的长度（单层部分与双层部分长度的和，其中调节扣所占的长度忽略不计）增长或缩短．经测量，得到如下数据：
单层部分的长度（cm） | … | 4 | 6 | 8 | 10 | … | 150 |
双层部分的长度（cm） | … | 73 | 72 | 71 |
| … | 0 |
（1）根据上表中数据的规律，填写表格中空白处的数据；
（2）设单层部分的长度为xcm，请用含x的代数式表示出双层部分的长度 cm；
（3）根据乐乐的身高和习惯，挎带的长度为110cm时，背起来最舒适，请求出此时单层部分的长度．
