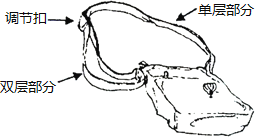
��Ŀ����
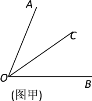
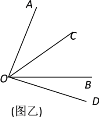
����Ŀ����ͼ����һ��б�����������˫�㲿�֡����㲿�ֺ͵��ڿ۹��ɣ������ú��֣�ͨ�����ڿۼӳ������̵��㲿�ֵij��ȣ�����ʹ����ij��ȣ����㲿����˫�㲿�ֳ��ȵĺͣ����е��ڿ���ռ�ij��Ⱥ��Բ��ƣ����������̣����������õ��������ݣ�
���㲿�ֵij��ȣ�cm�� | �� | 4 | 6 | 8 | 10 | �� | 150 |
˫�㲿�ֵij��ȣ�cm�� | �� | 73 | 72 | 71 | �� �� | �� | 0 |
��1�������ϱ������ݵĹ��ɣ���д�����пհ״������ݣ�
��2���赥�㲿�ֵij���Ϊxcm�����ú�x�Ĵ���ʽ��ʾ��˫�㲿�ֵij����� ��cm��
��3���������ֵ����ߺ�ϰ�ߣ�����ij���Ϊ110cmʱ�������������ʣ��������ʱ���㲿�ֵij��ȣ�
���𰸡���1��70����2��y����![]() x+75cm����3��70cm
x+75cm����3��70cm
��������
��1�����ݹ��ɼ��ɵó������
��2���۲�����֪��y��x��һ�κ�������y��kx+b�����ô���ϵ�������ɽ�����⣻
��3���г����̼��ɽ�����⣮
�⣺��1�����ݵ��㲿�ֵij���ÿ����2cm��˫�㲿�ֵij��ȼ�С1cm���ɵõ����㲿�ֵij���Ϊ10cmʱ��˫�㲿�ֵij���Ϊ70��
�ʴ�Ϊ��70��
��2���۲�����֪��y��x��һ�κ�������y��kx+b��
����![]() �����
�����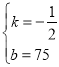 ��
��
��y����![]() x+75��
x+75��
�ʴ�Ϊ��y����![]() x+75��
x+75��
��3����������ã�
![]() ��
��
���x��70��
�𣺿���ij���Ϊ110cmʱ�����㲿�ֵij���Ϊ70cm��

 �����������һ��һ��ϵ�д�
�����������һ��һ��ϵ�д� Ӧ������ҵ��ϵ�д�
Ӧ������ҵ��ϵ�д�����Ŀ��ij��5�£��ҹ��Ϸ�ijʡA��B�����������غ����ֺ���1.5���˱���ת�ƣ��ڽ�����C��D��֪A��B���зֱ����������200�ֺ�300�ֵ���Ϣ������������֧Ԯ��������֪C���о�������240�֣�D���о�������260�֣��ֽ���Щ��������ȫ������A��B���У���֪��C������A��B���еķ��÷ֱ�Ϊÿ��20Ԫ��25Ԫ����D��������A��B���еķ��ñ�Ϊÿ��15Ԫ��30Ԫ�����D������B�еľ�������Ϊx�֣�
��1��������
A���֣� | B���֣� | �ϼƣ��֣� | |
C | �� �� | �� �� | 240 |
D | �� �� | x | 260 |
�ܼƣ��֣� | 200 | 300 | 500 |
��2����C��D���е����˷�ΪwԪ����w��x֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��3���������ޣ���D�е�B�е�·���õ��˸��ƣ�����������ʱ�䣬�˷�ÿ�ּ���mԪ��m��0��������·���˷Ѳ��䣮��C��D���е����˷ѵ���Сֵ��С��10320Ԫ����m��ȡֵ��Χ��