题目内容
【题目】问题探究:三角形的角平分线是初中几何中一条非常重要的线段,它除了具有平分角、角平分线上的点到角两边的距离相等这些性质外,还具有以下的性质:
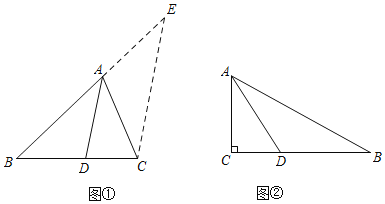
如图①,在△ABC中,AD平分∠BAC交BC于点D,则![]() =
=![]() .提示:过点C作CE∥AD交BA的延长线于点E.
.提示:过点C作CE∥AD交BA的延长线于点E.
请根据上面的提示,写出得到“![]() ”这一结论完整的证明过程.
”这一结论完整的证明过程.
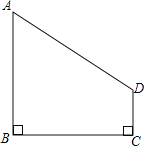
结论应用:如图②,在Rt△ABC中,∠C=90°,AC=8,BC=15,AD平分∠BAC交BC于点D.请直接利用“问题探究”的结论,求线段CD的长.
【答案】问题探究:见解析;结论应用:![]()
【解析】
问题探究:过点C作CE∥AD交BA的延长线于点E,可证∠BAD=∠E,∠DAC=∠ACE,由角平分线的性质可证AC=AE,结合平行线分线段成比例定理,即可得结论;
结论应用:由勾股定理可求AB的长,由![]() ,可求CD的长.
,可求CD的长.
问题探究:过点C作CE∥AD交BA的延长线于点E,
∴∠BAD=∠E,∠DAC=∠ACE,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴∠E=∠ACE,
∴AC=AE,
∵CE∥AD,
∴![]() ,
,
∴![]() ,
,
结论应用:在Rt△ABC中,∠C=90°,
∴AB![]() ,
,
设CD的长为x,则BD的长为15﹣x,
∵AD平分∠BAC,
∴![]()
∴![]()
解得:![]()
∴CD的长为:![]() .
.

【题目】某大学生创业团队有研发、管理和操作三个小组,各组的日工资和人数如下表所示.现从管理组分别抽调1人到研发组和操作组,调整后与调整前相比,下列说法中不正确的是( )
操作组 | 管理组 | 研发组 | |
日工资(元/人) | 260 | 280 | 300 |
人数(人) | 4 | 4 | 4 |
A.团队平均日工资不变B.团队日工资的方差不变
C.团队日工资的中位数不变D.团队日工资的极差不变
【题目】阅读理解 在研究函数![]() 的图象性质时,我们用“描点”的方法画出函数的图象.
的图象性质时,我们用“描点”的方法画出函数的图象.
列出表示几组![]() 与
与![]() 的对应值:
的对应值:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
描点连线:以表中各对对应值为坐标,描出各点,并用平滑的曲线顺次连接这些点,就得到函数![]() 的图象,如图1:
的图象,如图1:
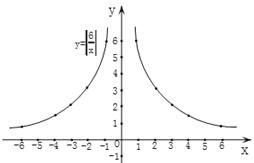
图1
可以看出,这个函数图象的两个分支分别在第一、二象限,且当![]() 时,与函数
时,与函数![]() 在第一象限的图象相同;当
在第一象限的图象相同;当![]() 时,与函数
时,与函数![]() 在第二象限的图象相同.类似地,我们把函数
在第二象限的图象相同.类似地,我们把函数![]() (
(![]() 是常数,
是常数,![]() )的图象称为“并进双曲线”.
)的图象称为“并进双曲线”.
认真观察图表,分别写出“并进双曲线”![]() 的对称性、函数的增减性性质:
的对称性、函数的增减性性质:
①图象的对称性性质: ;
②函数的增减性性质: ;
延伸探究如图2,点M,N分别在“并进双曲线”![]() 的两个分支上,
的两个分支上,![]() ,判断
,判断![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
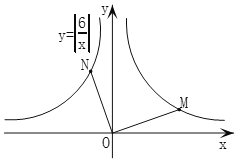
图2