题目内容
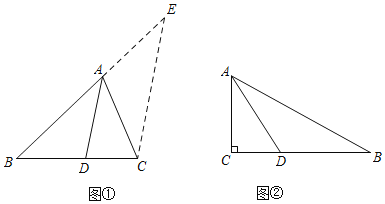
【题目】已知平行四边形ABCD,过点A作BC的垂线,垂足为点E,且满足AE=EC,过点C作AB的垂线,垂足为点F,交AE于点G,连接BG.

(1)如图1,若AC=![]() ,CD=4,求BC的长度;
,CD=4,求BC的长度;
(2)如图2取AC上一点Q,连接EQ,在△QEC内取一点,连接QH,EH,过点H作AC的垂线,垂足为点P,若QH=EH,∠QEH=45°.求证:AQ=2HP.
【答案】(1)3+![]() ;(2)见解析
;(2)见解析
【解析】
(1)利用勾股定理分别求出AE,BE即可解决问题.
(2)如图2中,如图2中,作EM⊥QE交QH的延长线于M,连接CM.证明△ABQ≌△CEM(SAS),推出AQ=CM,再利用三角形的中位线定理解决问题即可.
(1)解:如图1中,
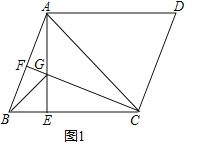
∵AE⊥BC于E,
∴∠AEC=90°,
∵AE=EC,AC=![]() ,
,
∴AE=EC=![]() ,
,
∵四边形ABCD是平行四边形,
∴AB=CD=4,
∵∠AEB=90°,
∴BE=![]() ,
,
∴BC=BE+EC=3+![]() .
.
(2)证明:如图2中,如图2中,作EM⊥QE交QH的延长线于M,连接CM.
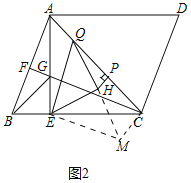
∵QH=EH,∠QEH=45°,
∴∠QEH=∠EQH=45°,
∴∠EHQ=90°,
∵EM⊥EQ,
∴∠MEQ=90°,
∴∠EMQ=∠EQM=45°,
∴EQ=EM,
∵EH⊥QM,
∴QH=HM,
∵∠AEC=∠QEM=90°,
∴∠AEQ=∠CEM,
∵EA=EC,EQ=EM,
∴△AEQ≌△CEM(SAS),
∴AQ=CM,∠EAQ=∠ECM=45°,
∵∠ACE=45°,
∴∠ACM=90°,
∵HP⊥QC,
∴∠HPQ=∠MCP,
∴HP∥CM,
∴QP=PC,
∵QH=HM,
∴CM=2PH,
∴AQ=2PH.

练习册系列答案
相关题目