��Ŀ����
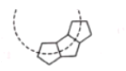
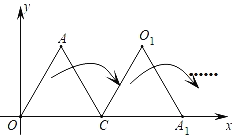
����Ŀ����ͼ����֪��A�ڵ�һ���ޣ���C������Ϊ��1��0������AOC�ǵȱ������Σ��ְѡ�AOC�����¹��ɽ�����ת����1����ת���ѡ�AOC�Ƶ�C��˳ʱ�뷽����ת120���õ���A1O1C����A1��O1�ֱ��ǵ�A��O�Ķ�Ӧ�㣬��2����ת���ѡ�A1O1C���ŵ�A1��˳ʱ�뷽����ת120���õ���A1O2C1����O2��C1�ֱ��ǵ�O1��C�Ķ�Ӧ�㣬��3����ת���ѡ�A1O2C1���ŵ�O2��˳ʱ�뷽����ת120���õ���A2O2C2����A2��C2�ֱ��ǵ�A1��C1�Ķ�Ӧ�㣬���������˹��ɣ���6����ת���ѡ�A3O4C3���ŵ�O4��˳ʱ�뷽����ת120���õ���A4O4C4����A4��C4�ֱ��ǵ�A3��C3�Ķ�Ӧ�㣬���A4�������ǣ�������
A.��![]() ��
��![]() ��B.��6��0��C.��
��B.��6��0��C.��![]() ��
��![]() ��D.��7��0��
��D.��7��0��
���𰸡�A
��������
�ֱ����A1A2��A3��A4�����꼴���жϣ�
������A1��2��0����A2��![]() ��
��![]() ����A3��5��
����A3��5��![]() ����A4��
����A4��![]() ��
��![]() ����
����
��ѡ��A��

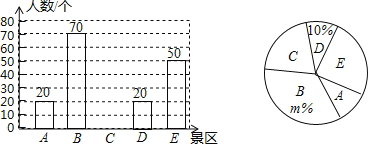
����Ŀ��ij��������һ����Ʒ���ɱ�ÿǧ��40Ԫ���涨ÿǧ���ۼ۲����ڳɱ����Ҳ�����80Ԫ�����г����飬ÿ���������y��ǧ�ˣ���ÿǧ���ۼ�x��Ԫ������һ�κ�����ϵ�������������±���
�ۼ�x��Ԫ/ǧ�ˣ� | 50 | 60 | 70 |
������y��ǧ�ˣ� | 100 | 80 | 60 |
��1����y��x֮��ĺ�������ʽ��
��2������Ʒÿ���������ΪW��Ԫ������W��x֮��ĺ�������ʽ���������멁�ɱ�����������ۼ�Ϊ����Ԫʱ������������������Ƕ��٣�