题目内容
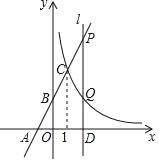
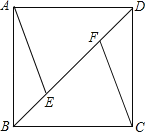
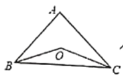
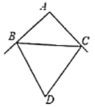
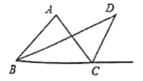
【题目】平面内有一等腰直角三角板(∠ACB=90°)和一直线MN,过点C作CE⊥MN于点E,过点B作BF⊥MN于点F.当点E与点A重合时(如图①),易证:AF+BF=2CE;当三角板绕点A顺时针旋转至图②、图③的位置时,上述结论是否仍然成立?若成立,请给予证明;若不成立,线段AF、BF、CE之间又有怎样的数量关系,请直接写出你的猜想,请直接写出你的猜想,不需证明.

【答案】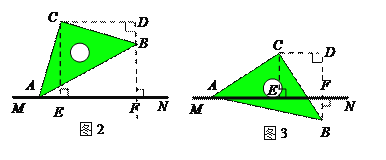
图2成立
过点C作CD⊥BF,交FB的延长线于点D
证出△AEC≌△BDC,∴CE=CD,AE=BD
证出四边形CEFD是正方形,∴CE=EF=DF
∴AF+BF=AE+EF+DF-BD,AF+BF=2CE
图3不成立
应为AF-BF=2CE
【解析】
过B作BH⊥CE与点H,易证△ACE≌△CBH,根据全等三角形的对应边相等,即可证得AF+BF=2CE.
图2,AF+BF=2CE仍成立,
证明:过B作BH⊥CE于点H,
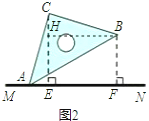
∵∠BCH+∠ACE=90°,
又∵在直角△ACE中,∠ACE+∠CAE=90°,
∴∠CAE=∠BCH,
又∵AC=BC,∠AEC=∠BHC=90°
∴△ACE≌△CBH.
∴CH=AE,BF=HE,CE=BH,
∴AF+BF=AE+EF+BF=CH+EF+HE=CE+EF=2EC.
图3中,过点C作CG⊥BF,交BF延长线于点G,
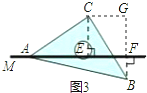
∵AC=BC,
可得∠AEC=∠CGB,
∠ACE=∠BCG,
∴△CBG≌△CAE,
∴AE=BG,
∵AF=AE+EF,
∴AF=BG+CE=BF+FG+CE=2CE+BF,
∴AF-BF=2CE.

【题目】垫球是排球队常规训练的重要项目之一,下列图表中的数据是运动员甲、乙、丙三人每人10次垫球测试的成绩,测试规则为每次连续接球10个,每垫球到位1个记1分,已知运动员甲测试成绩的中位数和众数都是7.
运动员甲测试成绩统计表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 |
| 6 | 8 | 6 | 8 |
|
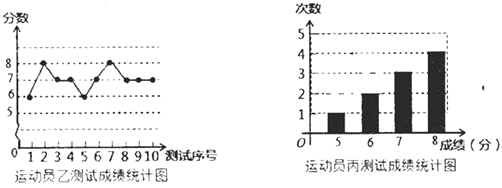
(1)填空:![]() ______;
______;![]() ______.
______.
(2)要从他们三人中选择一位垫球较为稳定的接球能手,你认为选谁更合适?为什么?