题目内容
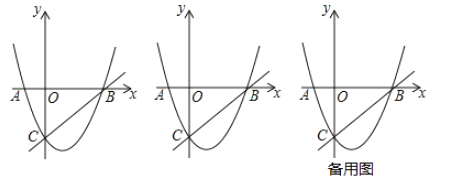
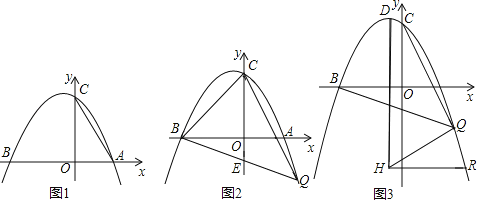
【题目】如图,抛物线y=ax2+bx+5经过坐标轴上A、B和C三点,连接AC,tanC=![]() ,5OA=3OB.
,5OA=3OB.
(1)求抛物线的解析式;
(2)点Q在第四象限的抛物线上且横坐标为t,连接BQ交y轴于点E,连接CQ、CB,△BCQ的面积为S,求S与t的函数解析式;
(3)已知点D是抛物线的顶点,连接CQ,DH所在直线是抛物线的对称轴,连接QH,若∠BQC=45°,HR∥x轴交抛物线于点R,HQ=HR,求点R的坐标.
【答案】(1)![]() ;(2)S=
;(2)S=![]() t2+
t2+![]() t;(3)点R(
t;(3)点R(![]() ﹣1,﹣6).
﹣1,﹣6).
【解析】
(1)c=5,OC=5,tanC=![]() ,则OA=3,5OA=3OB,则OB=5,故点A、B、C的坐标分别为:(3,0)、(﹣5,0)、(0,5),即可求解;
,则OA=3,5OA=3OB,则OB=5,故点A、B、C的坐标分别为:(3,0)、(﹣5,0)、(0,5),即可求解;
(2)S=![]() ×CE×(xQ﹣xB)=
×CE×(xQ﹣xB)=![]() ×(5+
×(5+![]() t﹣5)×(t﹣5)=
t﹣5)×(t﹣5)=![]() t2+
t2+![]() t;
t;
(3)证明△CTE≌△QTJ(AAS),故CE=QJ=5m,JN=JQ﹣QN=5m﹣3m=2m,tan∠EQN=tan∠JCN,即![]() ,解得:EN=m或﹣6m(舍去﹣6m);CN=CE+EN=5m+m=6m,故点Q(3m,5﹣6m),将点Q的坐标代入抛物线表达式并解得:m=0(舍去)或
,解得:EN=m或﹣6m(舍去﹣6m);CN=CE+EN=5m+m=6m,故点Q(3m,5﹣6m),将点Q的坐标代入抛物线表达式并解得:m=0(舍去)或![]() ,故点Q(4,﹣3),设:HR=k,则点R(k﹣1,﹣
,故点Q(4,﹣3),设:HR=k,则点R(k﹣1,﹣![]() k2+
k2+![]() ),
),
QS=yQ﹣yR=![]() k2﹣
k2﹣![]() ,由勾股定理得:QS2+HS2=HQ2,即(
,由勾股定理得:QS2+HS2=HQ2,即(![]() k2﹣
k2﹣![]() )2+25=k2,即可求解.
)2+25=k2,即可求解.
解:(1)由题意知c=5,
∴OC=5,
∵tanC=![]() ,
,
∴OA=3,
∵5OA=3OB,
∴OB=5,
故点A、B、C的坐标分别为:(3,0)、(﹣5,0)、(0,5),
则抛物线表达式为:y=a(x+5)(x﹣3)=a(x2+2x﹣15),
即﹣15a=5,解得:a=﹣![]() ,
,
故抛物线的表达式为:![]() ;
;
(2)设点Q(t,﹣![]() t2﹣
t2﹣![]() t+5),点B(﹣5,0),
t+5),点B(﹣5,0),
把点B、Q的坐标代入一次函数y=mx+n并解得:
直线BQ的表达式为:y=﹣![]() (t﹣3)(x+5),
(t﹣3)(x+5),
故点E(0,﹣![]() t+5),
t+5),
S=![]() ×CE×(xQ﹣xB)=
×CE×(xQ﹣xB)=![]() ×(5+
×(5+![]() t﹣5)×(t+5)=
t﹣5)×(t+5)=![]() t2+
t2+![]() t;
t;
(3)过点Q作QJ∥x轴交y轴于点N,交对称轴于点L,过点C作CT⊥BQ于点T,
延长CT交QJ于点J,过点Q作y轴的平行线交x轴于点K,交HR于点S,
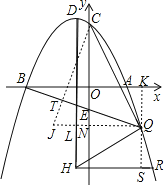
则OKQN为矩形,OK=QN=t,
由(2)知,CE=![]() t,故QN:CE=3:5,
t,故QN:CE=3:5,
设QN=3m,则CE=5m,
∵∠BQC=45°,故CT=QT,
∠EQN=90°﹣∠NEQ=90°﹣∠CET=∠TCE=∠JCN,
故△CTE≌△QTJ(AAS),
故CE=QJ=5m,JN=JQ﹣QN=5m﹣3m=2m,
tan∠EQN=tan∠JCN,即![]()
解得:EN=m或﹣6m(舍去﹣6m);
CN=CE+EN=5m+m=6m,故点Q(3m,5﹣6m),
将点Q的坐标代入抛物线表达式并解得:m=0(舍去)或![]() ,
,
故点Q(4,﹣3),
抛物线的顶点D坐标为:(﹣1,![]() ),
),
QL=4+1=5=HS,
设:HR=k,则点R(k﹣1,﹣![]() k2+
k2+![]() ),
),
QS=yQ﹣yR=![]() k2﹣
k2﹣![]() ,
,
由勾股定理得:QS2+HS2=HQ2,
即(![]() k2﹣
k2﹣![]() )2+25=k2,
)2+25=k2,
解得:k=![]() (不合题意值已舍去),
(不合题意值已舍去),
故点R(![]() ﹣1,﹣6).
﹣1,﹣6).