题目内容
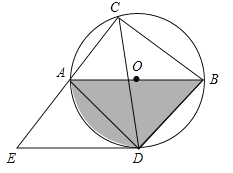
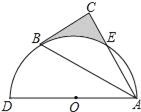
【题目】如图，以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点，交直角边AC于点E，B、E是半圆弧的三等分点，弧BE的长为
π，则图中阴影部分的面积为（ ）
A.
B.
C.
D.
【答案】D
【解析】
首先根据圆周角定理得出扇形半径以及圆周角度数，进而利用锐角三角函数关系得出BC，AC的长，利用S△ABC﹣S扇形BOE＝图中阴影部分的面积求出即可
解：连接BD，BE，BO，EO，
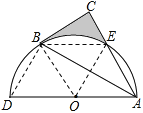
∵B，E是半圆弧的三等分点，
∴∠EOA＝∠EOB＝∠BOD＝60°，
∴∠BAC＝∠EBA＝30°，
∴BE∥AD，
∵弧BE的长为
π，
∴
＝π，
解得：R＝2，
∴AB＝ADcos30°＝2
，
∴BC＝
AB＝，
∴AC＝
＝3，
∴S△ABC＝×BC×AC＝××3＝
，
∵△BOE和△ABE同底等高，
∴△BOE和△ABE面积相等，
∴图中阴影部分的面积为：S△ABC﹣S扇形BOE＝﹣
＝﹣
．
故选D．
练习册系列答案
相关题目
