Question

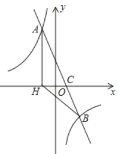
【题目】如图，抛物线经过两点，与轴交于点．

（1）求此抛物线的解析式；

（2）已知点为轴上一点，点关于直线的对称点为．

①当点刚好落在第四象限的抛物线上时，求出点的坐标；

②点在抛物线上，连接，是否存在点，使为等腰直角三角形？若存在，请直接写出点的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）；（2）①；②存在，（3，0）或（0，-3）或（4，5）或（，）或（2，-3）．

【解析】

（1）由点A、B的坐标，利用待定系数法即可求出抛物线的表达式；
（2）①可知△OBC为等腰直角三角形，求出点D′的纵坐标为-3，代入抛物线解析式可得CD=2，求出D点坐标；②可分别以P、D、D′为直角顶点画图，求出点P的坐标．

（1）∵抛物线经过两点

∴

解得

所以，抛物线的解析式

（2）①当x=0时，y=x2-2x-3=-3，
∴C（0，-3），
∵B（3，0），
∴OB=OC=3，
∴△OBC为等腰直角三角形，∠OCB=45°，
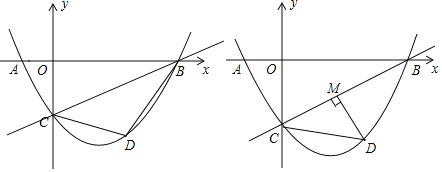
如图1，设D（0，t），

∵点关于直线的对称点为, 连接

∴由对称性可知：

∴轴

∴点的纵坐标为-3

当点在第四象限抛物线上时, 将代入，解得=2 , 或 =0 (舍去)

∴

∴

∴

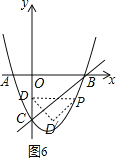
②分别以P、D、D′为直角顶点画图：
如图2，若以P为直角顶点，此时P与点B重合，则P（3，0），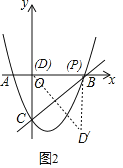

如图3，以P为直角顶点，此时点P与C重合，则P（0，-3），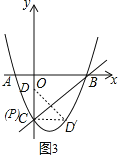

如图4以D为直角顶点，此时PC∥x轴，则P（2，-3），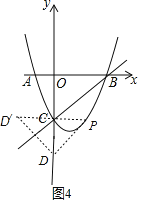

如图5，以D为直角顶点，此时PD′∥y轴，则P（4，5），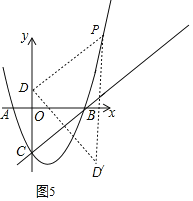

如图6，以D′为直角顶点，此时PD∥x轴，则P（，），

综上可得点P的坐标为（3，0）或（0，-3）或（4，5）或（，）或（2，-3）．