题目内容
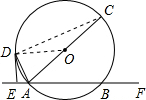
如图,直线EF交⊙O于A、B两点,AC是⊙O直径,DE是⊙O的切线,且DE⊥EF,垂足为E.
(1)求证:AD平分∠CAE;
(2)若DE=4cm,AE=2cm,求⊙O的半径.

(1)求证:AD平分∠CAE;
(2)若DE=4cm,AE=2cm,求⊙O的半径.

(1)证明:连接OD,
∵OD=OA,
∴∠ODA=∠OAD,(1分)
∵DE是⊙O的切线,
∴∠ODE=90°,OD⊥DE,(1分)
又∵DE⊥EF,
∴OD∥EF,(1分)
∴∠ODA=∠DAE,
∴∠DAE=∠OAD,
∴AD平分∠CAE;(2分)
(2)连接CD,
∵AC是⊙O直径,
∴∠ADC=90°,(1分)
在Rt△ADE中,DE=4cm,AE=2cm,
∴根据勾股定理得:AD=2
cm,(1分)
由(1)知:∠DAE=∠OAD,∠AED=∠ADC=90°,
∴△ADC∽△AED,
∴
=
,(1分)即
=
,
∴AC=10,(1分)
∴⊙O的半径是5.(1分)
∵OD=OA,
∴∠ODA=∠OAD,(1分)
∵DE是⊙O的切线,
∴∠ODE=90°,OD⊥DE,(1分)
又∵DE⊥EF,
∴OD∥EF,(1分)
∴∠ODA=∠DAE,
∴∠DAE=∠OAD,
∴AD平分∠CAE;(2分)
(2)连接CD,
∵AC是⊙O直径,
∴∠ADC=90°,(1分)
在Rt△ADE中,DE=4cm,AE=2cm,
∴根据勾股定理得:AD=2
| 5 |
由(1)知:∠DAE=∠OAD,∠AED=∠ADC=90°,
∴△ADC∽△AED,
∴
| AD |
| AE |
| AC |
| AD |
2
| ||
| 2 |
| AC | ||
2
|
∴AC=10,(1分)
∴⊙O的半径是5.(1分)


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
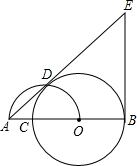







 线PBD过圆心,交⊙O于另一点D,连接CD.
线PBD过圆心,交⊙O于另一点D,连接CD.