题目内容
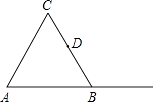
【题目】已知：如图，在Rt△ACB中，∠ACB=90°，点D是AB的中点，点E是CD的中点，过点C作CF∥AB叫AE的延长线于点F．
（1）求证：△ADE≌△FCE；
（2）若∠DCF=120°，DE=2，求BC的长．
【答案】（1）证明见解析；（2）4．
【解析】试题分析：（1）先根据点E是CD的中点得出DE=CE，再由AB∥CF可知∠BAF=∠AFC，根据AAS定理可得出△ADE≌△FCE；
（2）根据直角三角形的性质可得出AD=CD=
AB，再由AB∥CF可知∠BDC=180°﹣∠DCF=180°﹣120°=60°，由三角形外角的性质可得出∠DAC=∠ACD=∠BDC=30°，进而可得出结论．
试题解析：（1）证明：∵点E是CD的中点，∴DE=CE．
∵AB∥CF，∴∠BAF=∠AFC．
在△ADE与△FCE中，∵∠BAF=∠AFC，∠AED=∠FEC，DE=CE，∴△ADE≌△FCE（AAS）；
（2）解：由（1）得，CD=2DE，∵DE=2，∴CD=4．
∵点D为AB的中点，∠ACB=90°，∴AB=2CD=8，AD=CD=AB．
∵AB∥CF，∴∠BDC=180°﹣∠DCF=180°﹣120°=60°，∴∠DAC=∠ACD=∠BDC=×60°=30°，∴BC=AB=×8=4．
【题目】蔬菜经营户老王，近两天经营的是青菜和西兰花．
（1）昨天的青菜和西兰花的进价和售价如表，老王用600元批发青菜和西兰花共200市斤，当天售完后老王一共能赚多少元钱？
青菜 | 西兰花 | |
进价（元/市斤） | 2.8 | 3.2 |
售价（元/市斤） | 4 | 4.5 |
（2）今天因进价不变，老王仍用600元批发青菜和西兰花共200市斤．但在运输中青菜损坏了10%，而西兰花没有损坏仍按昨天的售价销售，要想当天售完后所赚的钱不少于昨天所赚的钱，请你帮老王计算，应怎样给青菜定售价？（精确到0.1元）
