��Ŀ����
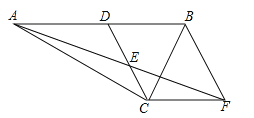
����Ŀ����ƽ��ֱ������ϵxOy�У�A��-1��0����B��1��0����C��0��1������DΪx���������ϵ�һ�����㣬��EΪ��һ������һ�㣬��CE��CD��CE=CD��
��1����˵������EBC����CAB ��
��2��ȡDE���е�F������OF�����ж�OF��AC��λ�ù�ϵ����˵�����ɣ�
��3���ڣ�2���������£���̽��O��D��F�����ܷɵ��������Σ����ܣ���ֱ��д�����з��������ĵ�D�����ꣻ�����ܣ���˵�����ɣ�

���𰸡���1��֤������������2��OF��AC����3��D(1��0)��D��1+![]() ��0��
��0��
��������
��1����֤��AOC����BOC��Ϊ����ֱ�������Σ��ҡ�ACD=��ECB���Ӷ��õ�
��ACD�ա�BCE����ȫ�������ζ�Ӧ����ȼ��ɵó����ۣ�
��2����FL��OC ��FK��OB����֤��CFL=��KFD��CF=DF=![]() DE���õ���CFL�ա�DFK����ȫ�������ζ�Ӧ����ȵõ�FL=FK���ɽ�ƽ�����ж������õ�OFƽ�֡�COB���Ӷ��õ���COF=��BOF=45�㣬���ɵõ�OF��AC��
DE���õ���CFL�ա�DFK����ȫ�������ζ�Ӧ����ȵõ�FL=FK���ɽ�ƽ�����ж������õ�OFƽ�֡�COB���Ӷ��õ���COF=��BOF=45�㣬���ɵõ�OF��AC��
��3����D��x��0��(x��0)����OD=x����E��EG��y����G�����EGC�ա�COD���õ�E�����������е����깫ʽ�õ�F�����������������빫ʽ�õ�OF��DF�ij���Ȼ������������������OD=OF����OD=FD����OF=FD��
��1����A��-1��0����B��1��0����C��0��1������AO=CO=BO=1��
��CO��AB����AC=BC����AOC����BOC��Ϊ����ֱ�������Σ����CBO=��BCO=��ACO=��CAO =45������ACB=90��������ACD+��BCD =90����
�֡�CE��CD�����ECB+��BCD =90�������ACD=��ECB��
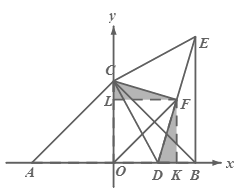
�ڡ�ACD���BCE�У���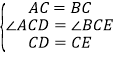 �����ACD�ա�BCE�����EBC����CAB��
�����ACD�ա�BCE�����EBC����CAB��
��2��OF��AC���������£�
��FL��OC ��FK��OB����ͼ����CO��BO�����LFK =90����
��CE=CD����F��DE���е㣬��CF��DE�����CFL+��LFD =90�㣮
�֡ߡ�KFD+��LFD =90�������CFL=��KFD��
��CE��CD����F��DE���е㣬��CF=DF=![]() DE��
DE��
�ڡ�CFL���DFK�У���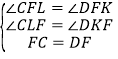 �����CFL�ա�DFK����FL=FK��
�����CFL�ա�DFK����FL=FK��
�֡�FL��OC ��FK��OB����OFƽ�֡�COB�����COF=��BOF=45�㣮
�֡ߡ�CAO =45������BOF=��CAO����OF��AC��
��3����D��x��0��(x��0)����OD=x����E��EG��y����G��
��CE��CD�����ECD=90�㣬���GCE+��DCO=90�㣮
�ߡ�GCE+��GEC=90�㣬���GEC=��OCD��
�ߡ�EGC=��COD=90�㣬CE=CD�����EGC�ա�COD����GE=OC=1��CG=OD=x����E��1��x+1����
��FΪED���е�����F(![]() ��
��![]() )����OF=
)����OF=![]() =
=![]() ��DF=
��DF=![]() =
=![]() ��
��
��ODF���������������������������
��OD=OF����x=![]() �������x=
�������x=![]() ����D(
����D(![]() ��0)��
��0)��
��OD=FD����x=![]() �������x=��1��������ȥ������x=1����D(1��0)��
�������x=��1��������ȥ������x=1����D(1��0)��
��OF=FD����![]() =
=![]() �������x=0(��ȥ)������������������
�������x=0(��ȥ)������������������
����������D(1��0)��D(![]() ��0)��
��0)��