题目内容
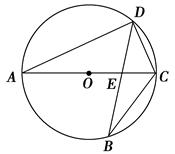
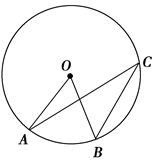
如图AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.

(1)若AB=2,∠P=30°,求AP的长;
(2)若D为AP的中点,求证:直线CD是⊙O的切线.

(1)若AB=2,∠P=30°,求AP的长;
(2)若D为AP的中点,求证:直线CD是⊙O的切线.
(1)2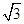 (2)证明见解析
(2)证明见解析
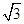 (2)证明见解析
(2)证明见解析(1)解:∵AB是⊙O的直径,AP是⊙O的切线,
∴AB⊥AP,∴∠BAP=90°;
又∵AB=2,∠P=30°,
∴AP=
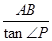 =
=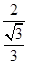 =2
=2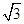 ,
,即AP=2
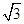 .
.(2)证明:如图,连接OC,OD、AC.
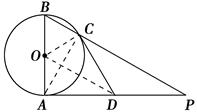
∵AB是⊙O的直径,
∴∠ACB=90°(直径所对的圆周角是直角),∴∠ACP=90°;
又∵D为AP的中点,
∴AD=CD(直角三角形斜边上的中线等于斜边的一半);
在△OAD和△OCD中,
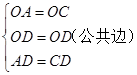 ,
,∴△OAD≌△OCD(SSS),
∴∠OAD=∠OCD(全等三角形的对应角相等);
又∵AP是⊙O的切线,A是切点,
∴AB⊥AP,
∴∠OAD=90°,
∴∠OCD=90°,即直线CD是⊙O的切线.

练习册系列答案
相关题目
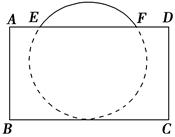
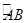 )对应的圆心角(∠AOB)为120°,OC的长为2cm,则三角板和量角器重叠部分的面积为 .
)对应的圆心角(∠AOB)为120°,OC的长为2cm,则三角板和量角器重叠部分的面积为 .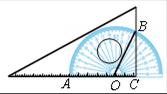
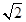 与⊙O的位置关系是( )
与⊙O的位置关系是( )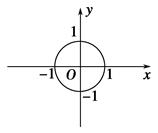
 B.
B.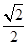
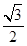 D.
D.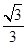
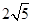 为半径的圆弧与x轴交于A,B两点,点A的坐标为(2,0),点B的坐标为(6,0),则圆心P的坐标为
为半径的圆弧与x轴交于A,B两点,点A的坐标为(2,0),点B的坐标为(6,0),则圆心P的坐标为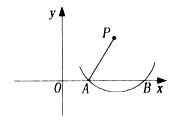
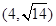
 )
)