题目内容
在平面直角坐标系内,已知点A(0,6)、点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.
(1)求直线AB的解析式;
(2)当t为何值时,以点A、P、Q为顶点的三角形与△AOB相似?
(3)当t=2秒时,四边形OPQB的面积为多少个平方单位?

(1)求直线AB的解析式;
(2)当t为何值时,以点A、P、Q为顶点的三角形与△AOB相似?
(3)当t=2秒时,四边形OPQB的面积为多少个平方单位?

(1)设直线AB的解析式为y=kx+b,
将点A(0,6)、点B(8,0)代入得
,
解得
,
直线AB的解析式为:y=-
x+6.
(2)∵Rt△OAB中,OA=6,OB=8,
∴由勾股定理可得,AB=10,
又知AP=t,AQ=10-2t.
分两种情况:
①当△APQ∽△AOB时,有:
=
,
∴
=
,解得t=
,
②当△AQP∽△AOB时,有:
=
,
∵
=
,解得t=
,
综上所述,当t=
或
时,
以点A、P、Q为顶点的三角形△AOB相似.
(3)当t=2秒时,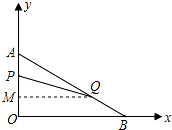
AP=2,AQ=6,过点Q作QM⊥OA于M,
易得△AMQ∽△AOB,
∴
=
,
=
,
解得QM=4.8,
∴△APQ的面积为:
AP×QM=
×2×4.8=4.8(平方单位),
∴四边形OPQB的面积为:S△AOB-S△APQ=24-4.8=19.2(平方单位).
将点A(0,6)、点B(8,0)代入得
|
解得
|
直线AB的解析式为:y=-
| 3 |
| 4 |
(2)∵Rt△OAB中,OA=6,OB=8,
∴由勾股定理可得,AB=10,
又知AP=t,AQ=10-2t.
分两种情况:
①当△APQ∽△AOB时,有:
| AP |
| AQ |
| AO |
| AB |
∴
| t |
| 10-2t |
| 6 |
| 10 |
| 30 |
| 11 |
②当△AQP∽△AOB时,有:
| AQ |
| AP |
| AO |
| AB |
∵
| 10-2t |
| t |
| 6 |
| 10 |
| 50 |
| 13 |
综上所述,当t=
| 30 |
| 11 |
| 50 |
| 13 |
以点A、P、Q为顶点的三角形△AOB相似.
(3)当t=2秒时,

AP=2,AQ=6,过点Q作QM⊥OA于M,
易得△AMQ∽△AOB,
∴
| AQ |
| AB |
| QM |
| OB |
| 6 |
| 10 |
| QM |
| 8 |
解得QM=4.8,
∴△APQ的面积为:
| 1 |
| 2 |
| 1 |
| 2 |
∴四边形OPQB的面积为:S△AOB-S△APQ=24-4.8=19.2(平方单位).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 直线ON上一动点(不与原点O重合),PM⊥x轴于M点.
直线ON上一动点(不与原点O重合),PM⊥x轴于M点.

 为
为