题目内容
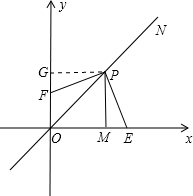
如图,在直角坐标系中,ON为过原点的一条直线,点E、F为x、y轴上的任意两点,P为 直线ON上一动点(不与原点O重合),PM⊥x轴于M点.
直线ON上一动点(不与原点O重合),PM⊥x轴于M点.
(1)若P(a,a)为直线ON上在第一象限内的任意一点,求直线ON的解析式;
(2)连接PE、PF,若∠PFO+∠PEO=180°,在(1)的条件下,试问线段PE与PF之间是否存在一定的数量关系,并说明理由;
(3)当P在直线ON上的第一象限内任意运动时,在(1)和(2)的条件下,
是否为定值?若是,求出这个定值;若不是,说明理由.
 直线ON上一动点(不与原点O重合),PM⊥x轴于M点.
直线ON上一动点(不与原点O重合),PM⊥x轴于M点.(1)若P(a,a)为直线ON上在第一象限内的任意一点,求直线ON的解析式;
(2)连接PE、PF,若∠PFO+∠PEO=180°,在(1)的条件下,试问线段PE与PF之间是否存在一定的数量关系,并说明理由;
(3)当P在直线ON上的第一象限内任意运动时,在(1)和(2)的条件下,
| OE+OF |
| OM |
(1)设直线ON的解析式为y=kx,P(a,a)代入得k=1,所以直线ON的解析式为y=x.
 (2)PE=PF.理由如下:
(2)PE=PF.理由如下:
如图,过P点作y轴的垂线交y轴于G点,则PG=PM,
又∵∠PFO+∠PEO=180,∴∠PFG=∠PEM,
∴直角△PGF≌直角△PME,所以PE=PF.
(3)
为定值2.
理由如下:由直角△PGF≌直角△PME,得OM=OG,ME=GF,
所以OE+OF=OM+ME+OG-GF=OM+ME+OM-ME=2OM,
所以
=2.
 (2)PE=PF.理由如下:
(2)PE=PF.理由如下:如图,过P点作y轴的垂线交y轴于G点,则PG=PM,
又∵∠PFO+∠PEO=180,∴∠PFG=∠PEM,
∴直角△PGF≌直角△PME,所以PE=PF.
(3)
| OE+OF |
| OM |
理由如下:由直角△PGF≌直角△PME,得OM=OG,ME=GF,
所以OE+OF=OM+ME+OG-GF=OM+ME+OM-ME=2OM,
所以
| OE+OF |
| OM |

练习册系列答案
相关题目