题目内容
如图,直线y=2x+4分别与x轴、y轴交于A、B两点,在此直线上有一点P,坐标是(-
,
),过点P的直线交y轴于点E,交x轴于点F,F点的坐标为(4,0).
(1)求直线EF的解析式.
(2)求证:AB=EF.
(3)请你判断△APF是否是直角三角形,并说出理由.

| 4 |
| 5 |
| 12 |
| 5 |
(1)求直线EF的解析式.
(2)求证:AB=EF.
(3)请你判断△APF是否是直角三角形,并说出理由.

(1)设直线EF的解析式为y=kx+b,
则有
,
解此方程组得:
,
∴直线EF的解析式为:y=-
x+2;
(2)直线y=2x+4别与x轴、y轴交点分别为A(-2,0),B(0,4),
∴OA=2,OB=4,
∴AB=
=2
,
∵直线y=-
x+2与y轴的交点E(0,2),
∴OE=2,
∵OF=4,
∴EF=
=2
,
∴AB=EF;
(3)△APF是直角三角形.
理由:在△OAB和△OEF中,
,
∴△OAB≌△OEF(SAS),
∴∠OFE=∠OBA,
∵∠OAB+∠OBA=90°,
∴∠OAB+∠OFE=90°,
∴∠APF=90°,
即△APF是直角三角形.
则有
|
解此方程组得:
|
∴直线EF的解析式为:y=-
| 1 |
| 2 |
(2)直线y=2x+4别与x轴、y轴交点分别为A(-2,0),B(0,4),
∴OA=2,OB=4,
∴AB=
| OA2+OB2 |
| 5 |
∵直线y=-
| 1 |
| 2 |
∴OE=2,
∵OF=4,
∴EF=
| OE2+OF2 |
| 5 |
∴AB=EF;
(3)△APF是直角三角形.
理由:在△OAB和△OEF中,
|
∴△OAB≌△OEF(SAS),
∴∠OFE=∠OBA,
∵∠OAB+∠OBA=90°,
∴∠OAB+∠OFE=90°,
∴∠APF=90°,
即△APF是直角三角形.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目




 着正方形的边,按O→A→B的顺序运动,设点P经过的路程为x,△OPB的面积为y.
着正方形的边,按O→A→B的顺序运动,设点P经过的路程为x,△OPB的面积为y.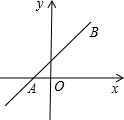
 轴正半轴于点Q(如图).
轴正半轴于点Q(如图).