题目内容
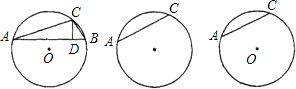
如图,在平面直角坐标系xoy中,⊙O1与x轴交于A、B两点,与y轴正半轴交于C点,已知A(-1,0),O1(1,0)
(1)求出C点的坐标.
(2)过点C作CD∥AB交⊙O1于D,连接BD,求证:四边形ABDC是等腰梯形.
(3)若过点C的直线恰好平分四边形ABCD的面积,求出该直线的解析式.

(1)求出C点的坐标.
(2)过点C作CD∥AB交⊙O1于D,连接BD,求证:四边形ABDC是等腰梯形.
(3)若过点C的直线恰好平分四边形ABCD的面积,求出该直线的解析式.

(1)∵A(-1,0),O1(1,0),
∴OA=OO1又O1A=O1C…1分,
∴易知△O1AC为等边三角形…2分,
∴易求C点的坐标为(0,
)…3分.
(2)证明:连接AD,
∵CD∥AB,
∴∠CDA=∠BAD,
∴
=
,
∴AC=BD,
∵直径AB于弦CD不等,
∴AC不平行BD,
∴四边形ABCD为等腰梯形…7分.
(3)解法一:过D作DH⊥AB于H,
∴△AOC≌△BDH,四边形COHD为矩形…8分,
∴CH必平分四边形ABCD的面积,
易求点H(2,0)…9分,
设直线CH的解析式为:y=kx+b,
则:
,
解得
…11分,
∴直线CH的解析式:y=-
x+
…12分.
解法二:设直线CH平分四边形ABCD的面积,并设H(x,0),
连接AD,
∵CD∥AB,
∴∠CDA=∠BAD,
∴
=
,
∴AC=BD=2,
∵S△ACH=S梯形CDBH,
∴
(x+1)=
[2+(3-x)],
∴x+1=5-x,
∴x=2,
由C(0,
)和H(2,0),易求CH的解析式:y=-
x+
.
∴OA=OO1又O1A=O1C…1分,
∴易知△O1AC为等边三角形…2分,
∴易求C点的坐标为(0,
| 3 |
(2)证明:连接AD,
∵CD∥AB,
∴∠CDA=∠BAD,
∴
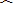 |
| AC |
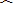 |
| BD |
∴AC=BD,
∵直径AB于弦CD不等,
∴AC不平行BD,
∴四边形ABCD为等腰梯形…7分.
(3)解法一:过D作DH⊥AB于H,
∴△AOC≌△BDH,四边形COHD为矩形…8分,
∴CH必平分四边形ABCD的面积,
易求点H(2,0)…9分,
设直线CH的解析式为:y=kx+b,
则:
|
解得
|
∴直线CH的解析式:y=-
| ||
| 2 |
| 3 |
解法二:设直线CH平分四边形ABCD的面积,并设H(x,0),
连接AD,
∵CD∥AB,
∴∠CDA=∠BAD,
∴
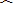 |
| AC |
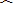 |
| BD |
∴AC=BD=2,
∵S△ACH=S梯形CDBH,
∴
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
∴x+1=5-x,
∴x=2,
由C(0,
| 3 |
| ||
| 2 |
| 3 |

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目