题目内容
如图在平面直角坐标系中,矩形OABC的边OC=6,对角线OB所在直线的函数解析式 为y=
为y=
x.
(1)直接写出C点的坐标;
(2)若D是BC边上的点,过D作DE⊥OB于E,已知DE=3.6.
①求出CD的长;
②以点C为圆心,CD长为半径作⊙C、试问在对角线OB上是否存在点P,使得以点P为圆心的⊙P与⊙C、x轴都相切?若存在,求出点P的坐标;若不存在,请说明理由.
 为y=
为y=| 3 |
| 4 |
(1)直接写出C点的坐标;
(2)若D是BC边上的点,过D作DE⊥OB于E,已知DE=3.6.
①求出CD的长;
②以点C为圆心,CD长为半径作⊙C、试问在对角线OB上是否存在点P,使得以点P为圆心的⊙P与⊙C、x轴都相切?若存在,求出点P的坐标;若不存在,请说明理由.
(1)C(0,6);
(2)①在矩形OABC中,∠OCB=90°,
∵OA=BC=8;
∴OB=
=10,
在△COB和△EDB中,∠CBO=∠EBD,∠OCB=90°=∠DEB,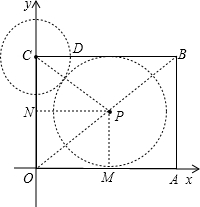
∴△COB∽△EDB,
∴
=
,
CD=2;
②如图,过P作PM⊥OA于M、PN⊥OC于N,设点P横坐标为m,
∵点P在直线y=
x上,
∴OM=NP=m,ON=MP=
m,
CN=6-
m,
当⊙P与⊙C外切、与x轴相切时,PC=
m+2,
在Rt△PCN中,PN2+CN2=PC2m2+(6-
m)2=(
m+2)2,
∴m2-12m+32=0,
解得m1=4,m2=8,
∴P1(4,3),P2(8,6),
同理,当⊙P与⊙C内切、与x轴相切时,m2+(6-
m)2=(
m-2)2m2-6m+32=0,
∵△=62-4×1×32<0,
∴此一元二次方程没有实数解,
使⊙P与⊙C内切、与x轴相切的点P不存在.
∴符合条件的点P是P1(4,3),P2(8,6).
(2)①在矩形OABC中,∠OCB=90°,
∵OA=BC=8;
∴OB=
| OC2+BC2 |
在△COB和△EDB中,∠CBO=∠EBD,∠OCB=90°=∠DEB,

∴△COB∽△EDB,
∴
| DE |
| OC |
| BD |
| BO |
CD=2;
②如图,过P作PM⊥OA于M、PN⊥OC于N,设点P横坐标为m,
∵点P在直线y=
| 3 |
| 4 |
∴OM=NP=m,ON=MP=
| 3 |
| 4 |
CN=6-
| 3 |
| 4 |
当⊙P与⊙C外切、与x轴相切时,PC=
| 3 |
| 4 |
在Rt△PCN中,PN2+CN2=PC2m2+(6-
| 3 |
| 4 |
| 3 |
| 4 |
∴m2-12m+32=0,
解得m1=4,m2=8,
∴P1(4,3),P2(8,6),
同理,当⊙P与⊙C内切、与x轴相切时,m2+(6-
| 3 |
| 4 |
| 3 |
| 4 |
∵△=62-4×1×32<0,
∴此一元二次方程没有实数解,
使⊙P与⊙C内切、与x轴相切的点P不存在.
∴符合条件的点P是P1(4,3),P2(8,6).

练习册系列答案
相关题目