题目内容
【题目】如图,边长一定的正方形ABCD,Q是CD上一动点,AQ交BD于点M,过M作MN⊥AQ交BC于N点,作NP⊥BD于点P,连接NQ,下列结论:①AM=MN;
②MP=![]() BD;③BN+DQ=NQ;④
BD;③BN+DQ=NQ;④![]() 为定值。其中一定成立的是_______.
为定值。其中一定成立的是_______.
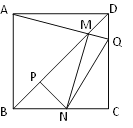
【答案】①②③④
【解析】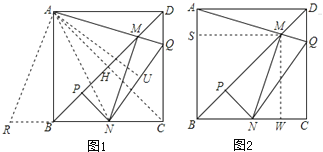
①如图1,作AU⊥NQ于U,交BD于H,连接AN,AC,
∵∠AMN=∠ABC=90°,
∴A,B,N,M四点共圆,
∴∠NAM=∠DBC=45°,∠ANM=∠ABD=45°,
∴∠ANM=∠NAM=45°,
∴AM=MN;
②由同角的余角相等知,∠HAM=∠PMN,
∴Rt△AHM≌Rt△MPN,
∴MP=AH=![]() AC=
AC=![]() BD;
BD;
③∵∠BAN+∠QAD=∠NAQ=45°,
∴在∠NAM作AU=AB=AD,且使∠BAN=∠NAU,∠DAQ=∠QAU,
∴△ABN≌△UAN,△DAQ≌△UAQ,有∠UAN=∠UAQ,BN=NU,DQ=UQ,
∴点U在NQ上,有BN+DQ=QU+UN=NQ;
④如图2,作MS⊥AB,垂足为S,作MW⊥BC,垂足为W,点M是对角线BD上的点,
∴四边形SMWB是正方形,有MS=MW=BS=BW,
∴△AMS≌△NMW
∴AS=NW,
∴AB+BN=SB+BW=2BW,
∵BW:BM=1: ![]() ,
,
∴![]() .
.
故答案为:①②③④

练习册系列答案
相关题目