题目内容
如图,点B是⊙O的半径OA的中点,且CD⊥OA于B,则tan∠CPD的值为( )
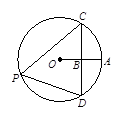

A.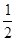 | B.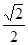 | C.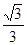 | D.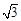 |
D
解答此题,需要将∠CPD转化到直角三角形中进行求解;连接OC、OD,由垂径定理和圆周角定理可得∠COB=∠CPD= 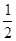 ∠COD,因此只需在Rt△OBC中求出∠COB的正弦值即可.
∠COD,因此只需在Rt△OBC中求出∠COB的正弦值即可.

解:连接OC、OD;
则∠COB=∠CPD=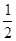 ∠COD;
∠COD;
Rt△OBC中,OC=2OB,则BC=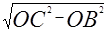 =
=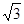 OB;
OB;
故tan∠CPD=tan∠COB=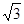 ;
;
故选D.
此题主要考查了圆周角定理、垂径定理以及勾股定理的综合应用.
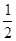 ∠COD,因此只需在Rt△OBC中求出∠COB的正弦值即可.
∠COD,因此只需在Rt△OBC中求出∠COB的正弦值即可.
解:连接OC、OD;
则∠COB=∠CPD=
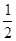 ∠COD;
∠COD;Rt△OBC中,OC=2OB,则BC=
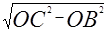 =
=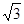 OB;
OB;故tan∠CPD=tan∠COB=
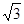 ;
;故选D.
此题主要考查了圆周角定理、垂径定理以及勾股定理的综合应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
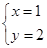 是方程x-ay=3的解,则a=-1
是方程x-ay=3的解,则a=-1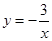 的图像上有两点(
的图像上有两点(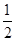 ,y1)(1,y2),则y1 <y2
,y1)(1,y2),则y1 <y2 的直径
的直径 过弦
过弦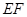 的中点
的中点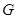 ,∠
,∠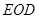 =
=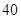 °,则∠
°,则∠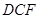 等于
等于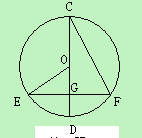
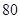 °
°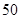 °
°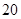 °
°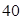 °
°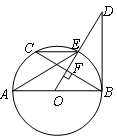
 置关系,并给出证明;
置关系,并给出证明;
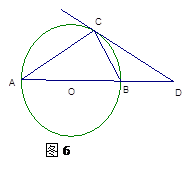
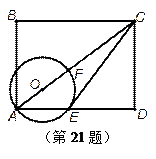
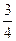 ,AE=7,求⊙O的直径.
,AE=7,求⊙O的直径.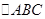 中,
中,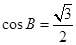 ,
,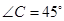 ,
,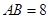 ,以点
,以点 为圆心4为半径的⊙
为圆心4为半径的⊙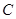 为圆心的⊙
为圆心的⊙