题目内容
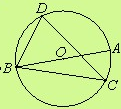
如图,在矩形ABCD中,点O在对角线AC上,以 OA长为半径的⊙O与AD、AC分别交于点E、F,且∠ACB=∠DCE.
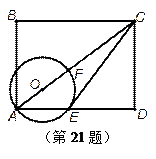
(1)求证:CE是⊙O的切线;
(2)若tan∠ACB=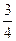 ,AE=7,求⊙O的直径.
,AE=7,求⊙O的直径.

(1)求证:CE是⊙O的切线;
(2)若tan∠ACB=
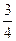 ,AE=7,求⊙O的直径.
,AE=7,求⊙O的直径.(1)证明略
(2)

(1)证明:连接OE,
∵ 四边形ABCD是矩形,
∴AD∥BC,∠D=90°.
∴∠3=∠1,∠2+∠5=90°. …………………………… 1分
又 OA=OE, ∴∠3=∠4.
∵∠1=∠2,
∴∠4=∠2. …………………………………………… 2分
∴∠4+∠5=90°,即∠OEC=90°.
∴OE⊥EC.
∴CE是⊙O的切线. ……………………………………… 3分
(2)解:连接EF,

∵AF是直径,∴∠AEF=90°.
∵ ∠ACB=∠3,
∴tan∠3=tan∠ACB=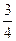 .………………………………………… 4分
.………………………………………… 4分
在RtΔAEF中,∵tan∠3= ,∴ cos∠3=
,∴ cos∠3= .
.
∴ AF= =
= . 即 ⊙O的直径等于
. 即 ⊙O的直径等于 . ………………… 5分
. ………………… 5分
∵ 四边形ABCD是矩形,
∴AD∥BC,∠D=90°.
∴∠3=∠1,∠2+∠5=90°. …………………………… 1分
又 OA=OE, ∴∠3=∠4.
∵∠1=∠2,
∴∠4=∠2. …………………………………………… 2分
∴∠4+∠5=90°,即∠OEC=90°.
∴OE⊥EC.
∴CE是⊙O的切线. ……………………………………… 3分
(2)解:连接EF,

∵AF是直径,∴∠AEF=90°.
∵ ∠ACB=∠3,
∴tan∠3=tan∠ACB=
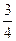 .………………………………………… 4分
.………………………………………… 4分在RtΔAEF中,∵tan∠3=
 ,∴ cos∠3=
,∴ cos∠3= .
.∴ AF=
 =
= . 即 ⊙O的直径等于
. 即 ⊙O的直径等于 . ………………… 5分
. ………………… 5分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
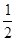
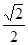
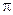 )
)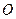 ,
, 点坐标为
点坐标为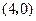 ,
,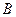 点坐标为
点坐标为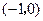 ,以
,以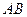 的中点
的中点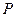 为圆心,
为圆心,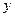 轴的正半轴交于点
轴的正半轴交于点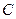 .
.
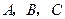 三点的抛物线对应的函数表达式.
三点的抛物线对应的函数表达式.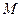 为(1)中抛物线的顶点,求直线
为(1)中抛物线的顶点,求直线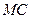 对应的函数表达式.
对应的函数表达式.
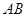 为
为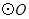 的直径,
的直径,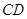 为
为