题目内容
已知⊙O1和⊙O2相切,它们的半径分别为3和1,过O1作⊙O2的切线,切点为A,则O1A的长是
连接过切点的半径,构造直角三角形,根据两圆内切或外切,得到两圆的圆心距,再根据勾股定理进行计算.
解:连接O2A,
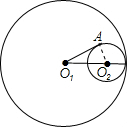
根据切线的性质,得∠O2AO1=90°,
根据两圆内切,得O1O2=3-1=2,
根据勾股定理,得O1A=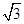 .
.
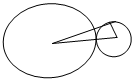
两圆若是外切
O1A=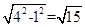
故答案为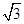 或
或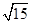
解:连接O2A,


根据切线的性质,得∠O2AO1=90°,
根据两圆内切,得O1O2=3-1=2,
根据勾股定理,得O1A=
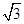 .
.两圆若是外切
O1A=
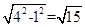
故答案为
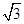 或
或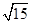

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
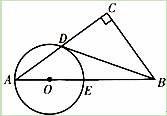




 )
)
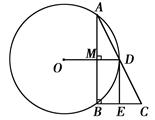
 ,求⊙O的直径。
,求⊙O的直径。