Question

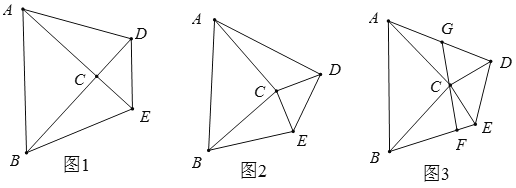
【题目】我们知道，如果两个三角形全等，则它们面积相等，而两个不全等的三角形，在某些情况下，可通过证明等底等高来说明它们的面积相等，已知与是等腰直角三角形，，连接、．

（1）如图1，当时，求证

（2）如图2，当时，上述结论是否仍然成立？如果成立，请证明；如果不成立，说明理由．

（3）如图3，在(2)的基础上，如果点为的中点，连接，延长交于，试猜想与的位置关系，并证明你的结论．

Answer 1

【答案】(1)证明见解析；(2)成立，理由见解析；(3) GF⊥BE，证明见解析

【解析】

(1)由△ABC和△DEC是等腰直角三角形，即可得出相应的线段相等，从而可以证明出；

(2)作AG垂直于DC的延长线于G，作BH垂直于CE，垂足为H，利用题目已知条件可证的△ACG≌△BCH，从而知道AG=BH，即可得出；

(3) 延长CG到点H，连接AH，根据题目已知可证的△AGH≌△DGC，得到CD=AH，∠AHG=∠HCD，进一步证的△AHC≌△ECB，得到∠CEB=∠AHC=∠HCD，最后利用互余即可证得GF⊥BE．

证明：(1)∵△ABC和△DEC是等腰直角三角形

∴AC=CB，DC=CE，∠ACB=∠DCE=90°

∵∠BCE=90°

∴∠ACD=90°

∵，

∴

(2)成立

如图所示，作AG垂直于DC的延长线于G，作BH垂直于CE，垂足为H

∵∠DCE=90°

∴∠GCE=90°

∵BH⊥CE

∴∠BHC=90°

∴GD∥BH

∴∠GCB=∠CBH

∵∠GCB+∠ACG=90°，∠BCH+∠CBH=90°

∴∠BCH=∠ACG

在△ACG和△BCH中

∴△ACG≌△BCH

∴AG=BH

∵，，CE=CD

∴

(3)GF⊥BE

如图所示，延长CG到点H，使得HG=GC，连接AH

∵点G为AD的中点

∴AG=GD

在△AGH和△DGC

∴△AGH≌△DGC

∴CD=AH，∠AHG=∠HCD

∴AH∥CD

∴∠HAC+∠ACD=180°

∵∠ACB=∠DCE=90°

∴∠ACD+∠BCE=180°

∴∠HAC=∠BCE

∵△DCE是等腰三角形

∴CD=CE

∴CE=AH

在△AHC和△ECB中

∴△AHC≌△ECB

∴∠CEB=∠AHC=∠HCD

∵∠HCD+∠FCE=90°

∴∠FCE+∠CEF=90°

∴∠CFE=90°

∴GF⊥BE