题目内容
【题目】如图,AB是⊙O的直径,BC交⊙O于点D,E是![]() 的中点,AE与BC交于点F,∠C=2∠EAB.
的中点,AE与BC交于点F,∠C=2∠EAB.
(1)求证:AC是⊙O的切线;
(2)已知CD=4,CA=6,
①求CB的长;
②求DF的长.
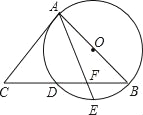
【答案】(1)证明见解析;(2) ①BC=9;②DF=2.
【解析】
(1) 连结AD, 根据圆周角定理,由E是BD的中点得到∠EAB=∠EAD, 由于∠ACB=2∠EAB, 则∠ACB=∠DAB, 再利用圆周角定理得到∠ADB=![]() , 则∠DAC+∠ACB=90, 所以∠DAC+∠DAB=
, 则∠DAC+∠ACB=90, 所以∠DAC+∠DAB=![]() , 于是根据切线的判定定理得到AC是OO的切线;
, 于是根据切线的判定定理得到AC是OO的切线;
(2)①在Rt△ABC中, 根据cosC=![]() =
=![]() =
=![]() ,AC=6可得AC=6;
,AC=6可得AC=6;
②作FH⊥AB于H, 由BD=BC-CD=5, ∠EAB=∠EAD, FD⊥AD,FH⊥AB, 推出FD=FH, 设FB=x, 则DF=FH=5-x, 根据cos∠BFH=cos∠C=![]() =
=![]() ,构建方程即可解决问题.
,构建方程即可解决问题.
(1)连结AD,如图,
∵E是![]() 的中点,
的中点,
∴![]() =
=![]() =,
=,
∴∠EAB=∠EAD,
∵∠ACB=2∠EAB,
∴∠ACB=∠DAB,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠DAC+∠ACB=90°,
∴∠DAC+∠DAB=90°,即∠BAC=90°,
∴AC⊥AB,
∴AC是⊙O的切线;
(2)①在Rt△ACB中,
∵cosC=![]() =
=![]() =
=![]() ,AC=6,
,AC=6,
∴BC=9.
②作FH⊥AB于H,
∵BD=BC﹣CD=5,∠EAB=∠EAD,FD⊥AD,FH⊥AB,
∴FD=FH,设FB=x,则DF=FH=5﹣x,
∵FH∥AC,
∴∠HFB=∠C,
在Rt△BFH中,
∵cos∠BFH=cos∠C=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得x=3,即BF的长为3,
∴DF=2

练习册系列答案
相关题目