题目内容
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,给出下列结论:①b2=4ac,②abc<0;③a>c;④4a﹣2b+c<0,其中正确的个数有( )
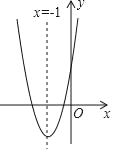
A. 1个 B. 2个 C. 3个 D. 4个
【答案】A
【解析】
根据二次函数的图象和二次函数的性质可以判断各个小题中的结论是否成立,从而可以解答本题.
∵函数图象与x轴两个交点,∴b2﹣4ac>0,即b2>4ac,故①错误.
∵抛物线顶点在y轴左侧,与y轴交于正半轴,∴ab>0,c>0,则abc>0,故②错误.
∵![]() ,则b=2a.
,则b=2a.
∵x=﹣1时,y=a﹣b+c<0,则a﹣2a+c<0,得a>c,故③正确;
当x=﹣2与x=0时的函数值相等,则x=﹣2时,y=4a﹣2b+c>0,故④错误.
故选A.

练习册系列答案
相关题目