题目内容
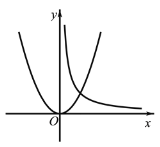
【题目】平面直角坐标系中,直线y=2kx-2k (k>0)交y轴于点B,与直线y=kx交于点A.
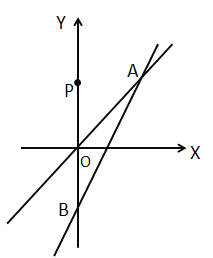
(1)求点A的横坐标;
(2)直接写出![]() 的x的取值范围;
的x的取值范围;
(3)若P(0,3)求PA+OA的最小值,并求此时k的值;
(4)若C(0,2)以A,B,C,D为顶点的四边形是以BC为一条边的菱形,求k的值.
【答案】(1)![]() 点横坐标为2;(2)
点横坐标为2;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]() 或
或![]() .
.
【解析】
(1)联立两直线方程即可得出答案;
(2)先根据图像求出k的取值范围,再解不等式组即可得出答案;
(3)先求出点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() 的坐标,连接
的坐标,连接![]() 交直线
交直线![]() 于点
于点![]() ,此时
,此时![]() 最小,根据将
最小,根据将![]() 和P的坐标求出直线
和P的坐标求出直线![]() 的解析式,再令x=2,求出y的值,即可得出点A的坐标,再将点A的坐标代入y=kx中即可得出答案;
的解析式,再令x=2,求出y的值,即可得出点A的坐标,再将点A的坐标代入y=kx中即可得出答案;
(4)根据题意得出△ABC为等腰三角形,且BC为腰,再根据A、B和C的坐标分别求出AB、BC和AC的长度,分情况进行讨论:①当![]() 时,②当
时,②当![]() 时,即可得出答案.
时,即可得出答案.
解:(1)根据题意得
![]() ,解得
,解得![]()
![]() 点横坐标为2;
点横坐标为2;
(2)由图像可知k>0
∴由2kx-2k>0,可得x>1;由2kx-2k<kx,得x<2,
∴![]()
(3)如图,点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ;
;
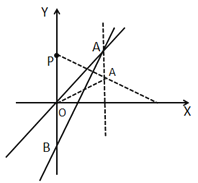
连接![]() 交直线
交直线![]() 于点
于点![]() ,此时
,此时![]() 最小,
最小,
其值为![]() ;
;
设直线![]() 的解析式为y=ax+b
的解析式为y=ax+b
将![]() 和P的坐标代入得:
和P的坐标代入得:![]()
解得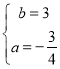
∴直线![]() 的解析式为
的解析式为![]() ,
,
当x=2时,y=![]()
![]() .即
.即![]() ,
,![]() ;
;
(4)![]() 以
以![]() 为顶点的四边形是以
为顶点的四边形是以![]() 为一条边的菱形,
为一条边的菱形,
![]() 为等腰三角形,且
为等腰三角形,且![]() 为腰;
为腰;
![]() 或
或![]() ,
,
![]()
①当![]() 时,
时,![]() ,
,![]() ,解得
,解得![]() ;
;
②当![]() 时,
时,![]() ,
,![]() ,
,
解得![]() .
.
![]() 或
或![]()

练习册系列答案
相关题目