题目内容
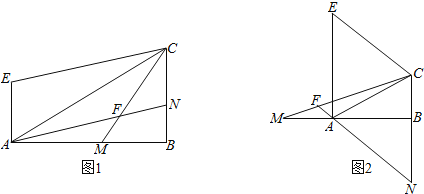
【题目】Rt△ABC中,∠ABC=90°,在直线AB上取一点M,使AM=BC,过点A作AE⊥AB且AE=BM,连接EC,再过点A作AN∥EC,交直线CM、CB于点F、N.
(1)如图1,若点M在线段AB边上时,求∠AFM的度数;
(2)如图2,若点M在线段BA的延长线上时,且∠CMB=15°,求∠AFM的度数.
【答案】(1) 45°;(2) 120°.
【解析】
(1)如图1,连接EM.根据AE⊥AB,AE=MB,AM=CB,可求出△AEM≌△BMC;根据直角三角形的性质可知△EMC是等腰直角三角形;再结合平行线的性质可知∠AFM=45°.
(2)如图2,连接EM.同(1)△AEM≌△BMC,则EM=MC,∠MEA=∠CMB=15°.易证△EMC是等边三角形,故∠ECM=60°,又由AN∥CE得到:∠AFM=∠ECM=60°.
(1)连接EM.
∵AE⊥AB,∴∠EAM=∠B=90°.
在△AEM与△BMC中,
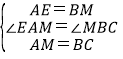 ,
,
∴△AEM≌△BMC(SAS).
∴∠AEM=∠BMC,EM=MC.
∵∠AEM+∠AME=90°,
∴∠BMC+∠AME=90.
∴∠EMC=90°.
∴△EMC是等腰直角三角形.
∴∠MCE=45°
∵AN∥CE,
∴∠AFM=∠MCE=45°;
(2)如图2,连接ME.
同(1)△AEM≌△BMC(SAS),则EM=MC,∠MEA=∠CMB=15°.
又∵∠MEA+∠EMA=90°,
∴∠EMC=60°,
∴△EMC是等边三角形,
∴∠ECM=60°,
∵AN∥CE
∴∠AFM+∠ECM=180°,
∴∠AFM=120°.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目