题目内容
【题目】某同学在平时的练习中,遇到下面一道题目:
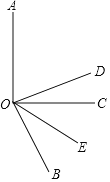
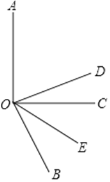
如图,∠AOC=90°,OE 平分∠BOC,OD平分∠AOB.
①若∠BOC=60°,求∠DOE 度数;
②若∠BOC=α(0<α<90°),其他条件不变,求∠DOE 的度数.
(1)下面是某同学对①问的部分解答过程,请你补充完整.
∵OE 平分∠BOC,∠BOC=60°
∴∠BOE= . (角平分线的定义)
∵∠AOC=90°,∠BOC=60°
∴ ,
∵OD 平分∠AOB,
∴ ,(角平分线的定义)
∴∠DOE= .
(注:符号∵表示因为,用符号∴表示所以).
(2)仿照①的解答过程,完成第②小题.
【答案】(1)45°;(2)45°.
【解析】
(1)根据∠AOC、∠BOC的度数可得出∠AOB的度数,根据角平分线的定义即可得出∠BOE、∠BOD的度数,再根据∠DOE与∠BOE、∠BOD之间的关系通过角的计算即可得出结论;
(2)根据∠AOC、∠BOC的度数可得出∠AOB的度数,根据角平分线的定义即可得出∠BOE、∠BOD的度数,再根据∠DOE与∠BOE、∠BOD之间的关系通过角的计算即可得出结论.
(1) ∵OE 平分∠BOC,∠BOC=60°
∴∠BOE= 30° . (角平分线的定义)
∵∠AOC=90°,∠BOC=60°
∴ ∠AOB=150° ,
∵OD 平分∠AOB,
∴ ∠BOD=75° ,(角平分线的定义)
∴∠DOE= 45° .
(2)
∵OE 平分∠BOC,∠BOC=α.
∴∠BOE=![]() (角平分线的定义)
(角平分线的定义)
∵∠AOC=90°,∠BOC=α
∴![]() ,
,
∵OD 平分∠AOB,
∴∠BOD=![]() ,(角平分线的定义)
,(角平分线的定义)
∴∠DOE=45°.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目