Question

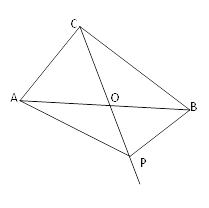
【题目】已知：如图，在Rt△ABC中，∠C=90°，AD是△ABC的角平分线，DE⊥AB，垂足为点E，AE=BE．

（1）求∠B的度数；

（2）如果AC=3cm，CD=cm，求△ABD的面积．

Answer 1

【答案】（1）∠B=30°；（2）3cm2．

【解析】

（1）根据已知条件得到AD=BD，由等腰三角形的性质得到∠B=∠DAE，根据AD是△ABC的角平分线，求得∠DAE=∠DAC，于是得到∠B=∠DAE=∠DAC，列方程即可得到结论；

（2）根据已知条件求得Rt△ACD≌Rt△AED，根据全等三角形的性质得到AE=AC，DE=CD，于是得到AB，即可得到结论．

（1）∵DE⊥AB且AE=BE，

∴AD=BD，

∴∠B=∠DAE，

∵AD是△ABC的角平分线，

∴∠DAE=∠DAC，

∴∠B=∠DAE=∠DAC，

∵∠C=90°，

∴∠B+∠DAE+∠DAC=90°，

∴∠B=30°；

（2）∵∠C=90°，AD是△ABC的角平分线，DE⊥AB，

在Rt△ACD与Rt△AED中，

，

∴Rt△ACD≌Rt△AED，（HL），

∴AE=AC=3cm，DE=CD=cm，

∵AE=BE，

∴AB=2AE=2×3=6，

∴S△ABD=ABDE=×6×=3cm2．