题目内容
如图,已知函数 的图象与y轴交于点A,一次函数
的图象与y轴交于点A,一次函数 的图象 经过点B(0,-1),并且与x轴以及
的图象 经过点B(0,-1),并且与x轴以及 的图象分别交于点C、D.
的图象分别交于点C、D.

(1)若点D的横坐标为1,求四边形AOCD的面积(即图中阴影部分的面积);
(2)在第(1)小题的条件下,在y轴上是否存在这样的点P,使得以点P、B、D为顶点的三角形是等腰三角形.如果存在,求出点P坐标;如果不存在,说明理由.
(3)若一次函数 的图象与函数
的图象与函数 的图象的交点D始终在第一象限,则系数k的取值范围是 .(请直接写出结果)
的图象的交点D始终在第一象限,则系数k的取值范围是 .(请直接写出结果)
 的图象与y轴交于点A,一次函数
的图象与y轴交于点A,一次函数 的图象 经过点B(0,-1),并且与x轴以及
的图象 经过点B(0,-1),并且与x轴以及 的图象分别交于点C、D.
的图象分别交于点C、D.
(1)若点D的横坐标为1,求四边形AOCD的面积(即图中阴影部分的面积);
(2)在第(1)小题的条件下,在y轴上是否存在这样的点P,使得以点P、B、D为顶点的三角形是等腰三角形.如果存在,求出点P坐标;如果不存在,说明理由.
(3)若一次函数
 的图象与函数
的图象与函数 的图象的交点D始终在第一象限,则系数k的取值范围是 .(请直接写出结果)
的图象的交点D始终在第一象限,则系数k的取值范围是 .(请直接写出结果)(1) ;(2)满足条件的点P有4个:
;(2)满足条件的点P有4个: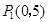 、
、 、
、 、
、 ;(3)
;(3) .
.
 ;(2)满足条件的点P有4个:
;(2)满足条件的点P有4个: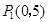 、
、 、
、 、
、 ;(3)
;(3) .
.试题分析:本题考查了一次函数综合知识,难度适中,关键是掌握分类讨论思想的运用.(1)如图,连接OD,先求出点D的坐标,再求出BD的解析式,然后根据S四边形AOCD=S△AOD+S△COD即可求解;
(2)求使得以点P、B、D为顶点的三角形是等腰三角形.分三种情况讨论:①当DP=DB时;②当BP=DB时;③当PB=PD时。在三种情况下分别求出点P的坐标.
(3)交点D始终在第一象限,即点D的横坐标x>0.可由交点得到:kx-1=x+1,解得
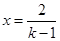 ,由此可得
,由此可得 ;实际上本题可直接根据图象得出答案.
;实际上本题可直接根据图象得出答案.
试题解析:
解:(1)∵点D的横坐标为1,点D在y=x+1的图象上,
∴D(1,2),
∴直线BD的解析式为y=3x-1,
∴A(0,1),C(13,0),
∴


应分三种情况讨论:如图,
①当DP=DB时,点D位于BP的垂直平分线上,过点D作DE⊥y轴,则BE=PE
∵B(0,-1),D(1,2),
∴BE=BO+OE=1+2=3
∴PE=3
∴PO=5
∴点P的坐标为:
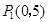
②当BP=DB时,

∴
 ,
,
③当PB=PD时,点P位于BD的垂直平分线与y轴的交点上,设P(0,a),
则(a+1)2=1+(2-a)2,
解得:

∴

(3)若一次函数y=kx+b的图象与函数y=x+1的图象的交点D始终在第一象限,则系数k的取值范围是:k>1.

练习册系列答案
相关题目
 与
与 轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).将直线
轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).将直线


 与直线
与直线 相交于点A(4,m)、B.
相交于点A(4,m)、B.
 ?(直接写出答案)
?(直接写出答案)