题目内容
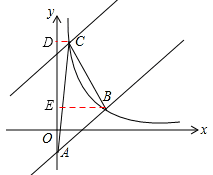
如图,在平面直角坐标系中直线 与
与 轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).将直线
轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).将直线 向上平移后与反比例函数图象在第一象限内交于点C,且△ABC的面积为18,求平移后的直线的函数关系式是 .
向上平移后与反比例函数图象在第一象限内交于点C,且△ABC的面积为18,求平移后的直线的函数关系式是 .

 与
与 轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).将直线
轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).将直线 向上平移后与反比例函数图象在第一象限内交于点C,且△ABC的面积为18,求平移后的直线的函数关系式是 .
向上平移后与反比例函数图象在第一象限内交于点C,且△ABC的面积为18,求平移后的直线的函数关系式是 .
y=x+7.
试题分析:将B坐标代入直线y=x﹣2中得:m﹣2=2,解得:m=4,∴B(4,2),即BE=4,OE=2.
设反比例解析式为
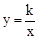 ,将B(4,2)代入反比例解析式得:k=8,∴反比例解析式为
,将B(4,2)代入反比例解析式得:k=8,∴反比例解析式为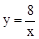 .
.设平移后直线解析式为y=x+b,C(a,a+b),
对于直线y=x﹣2,令x=0求出y=﹣2,得到OA=2,
如图,过C作CD⊥y轴,过B作BE⊥y轴,
将C坐标代入反比例解析式得:a(a+b)=8①,
∵
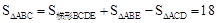 ,∴
,∴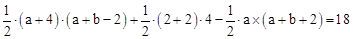 ②.
②.①②联立,解得:b=7.
∴平移后直线解析式为y=x+7.

练习册系列答案
相关题目
 +2与x轴、y轴分别交于A、B两点,以AB为边在第二象限内作正方形ABCD.
+2与x轴、y轴分别交于A、B两点,以AB为边在第二象限内作正方形ABCD.
 的图象与y轴交于点A,一次函数
的图象与y轴交于点A,一次函数 的图象 经过点B(0,-1),并且与x轴以及
的图象 经过点B(0,-1),并且与x轴以及
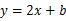 与两个坐标轴围成的三角形面积为4,则
与两个坐标轴围成的三角形面积为4,则 ________.
________.


 的函数
的函数 和
和 在同一坐标系中的图像大致是( )
在同一坐标系中的图像大致是( )

