��Ŀ����
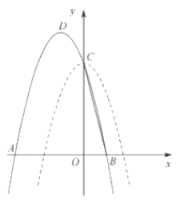
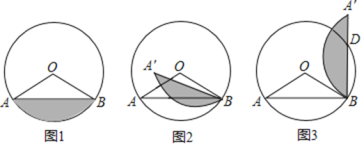
����Ŀ����ͼ����֪������![]() ����������
����������![]() ��
��![]() �ᷭ�ۣ��õ�������
�ᷭ�ۣ��õ�������![]() ��
��
��1�����������![]() �ĺ�������ʽ��
�ĺ�������ʽ��
��2���ֽ�������![]() ����ƽ��
����ƽ��![]() ����λ���ȣ�ƽ�ƺ�õ����������ߵĶ���Ϊ
����λ���ȣ�ƽ�ƺ�õ����������ߵĶ���Ϊ![]() ����
����![]() ��Ľ������������Ϊ
��Ľ������������Ϊ![]() ��
��![]() ����������
����������![]() ����Ҳƽ��
����Ҳƽ��![]() ����λ���ȣ�ƽ�ƺ�õ����������ߵĶ���Ϊ
����λ���ȣ�ƽ�ƺ�õ����������ߵĶ���Ϊ![]() ����
����![]() �ύ�����������Ϊ
�ύ�����������Ϊ![]() ��
��![]() ����ƽ�ƹ����У��Ƿ�����Ե�
����ƽ�ƹ����У��Ƿ�����Ե�![]() ��
��![]() ��
��![]() ��
��![]() Ϊ������ı����Ǿ��ε����Σ������ڣ��������ʱ
Ϊ������ı����Ǿ��ε����Σ������ڣ��������ʱ![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
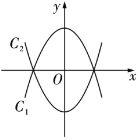

���𰸡���1��![]() ����2�����ڣ���
����2�����ڣ���![]() ʱ���Ե�
ʱ���Ե�![]() ��
��![]() ��
��![]() ��
��![]() Ϊ������ı����Ǿ��Σ�
Ϊ������ı����Ǿ��Σ�
��������
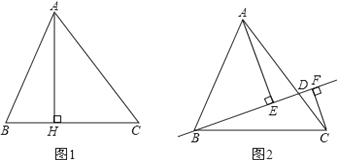
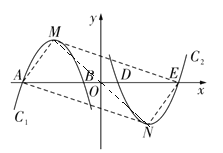
��1�������߷���ǰ�����x��Գƣ�a��Ϊ�෴����
��2������AN��NE��EM��MA��M��N����ԭ��O�Գ�OM��ON��A��E����ԭ��O�Գ�OA��OE���ж��ı���ANEMΪƽ���ı��Σ���AM2��ME2��AE2�����m��3��������⣮
�⣺��1����������![]() �Ķ���Ϊ
�Ķ���Ϊ![]() ��
��
����![]() �ᷭ�ۺ������Ϊ
�ᷭ�ۺ������Ϊ![]() ��
��
��������![]() �ĺ�������ʽΪ
�ĺ�������ʽΪ![]() ��
��
��2�����ڣ�
���ɣ�����![]() ��
��![]() ��
��![]() ��
��![]() ��������ɵã�
��������ɵã�![]() ��
��![]() ��
��
��![]() ��
��![]() ����ԭ��
����ԭ��![]() �Գƣ���
�Գƣ���![]() ��
��
ԭ![]() ��
��![]() ��������
��������![]() �����������ֱ�Ϊ
�����������ֱ�Ϊ![]() ��
��![]() ��
��
��![]() ��
��![]() ����
����![]() ��
��![]() ����ԭ��
����ԭ��![]() �Գƣ���
�Գƣ���![]() ��
��
���ı���![]() Ϊƽ���ı��Σ�
Ϊƽ���ı��Σ�
![]() ��
��
![]() ��
��
![]() ��
��
��![]() ����
����![]() �����
�����![]() ��
��
��ʱ![]() ��ֱ�������Σ���
��ֱ�������Σ���![]() ��
��
����![]() ʱ���Ե�
ʱ���Ե�![]() ��
��![]() ��
��![]() ��
��![]() Ϊ������ı����Ǿ��Σ�
Ϊ������ı����Ǿ��Σ�

����Ŀ��Ϊ�˹��������ܱߵ�ũ����ֲ˵Ļ����ԣ�ij��˾�ƻ��½�![]() ��
��![]() ��������80���������۸�ũ���ֲˣ���֪��1��
��������80���������۸�ũ���ֲˣ���֪��1��![]() �����Һ�2��
�����Һ�2��![]() ������һ����Ҫ8.1��Ԫ���������ҵijɱ��ͳ��ۼ����±���
������һ����Ҫ8.1��Ԫ���������ҵijɱ��ͳ��ۼ����±���
|
| |
�ɱ�����Ԫ/���� | 2.5 |
|
���ۼۣ���Ԫ/���� | 3.1 | 3.5 |
��1����![]() ��ֵ��
��ֵ��
��2����֪�½�![]() �����Ҳ�����38��������50�����������������ҿ�ȫ���۳���Ϊ�˼����ũ���������ʲ���ʲô�����������ҿ�ʹ�������٣����������Ƕ��٣�
�����Ҳ�����38��������50�����������������ҿ�ȫ���۳���Ϊ�˼����ũ���������ʲ���ʲô�����������ҿ�ʹ�������٣����������Ƕ��٣�