题目内容
（11·肇庆）如图3，四边形ABCD是圆内接四边形，E是BC延长线上一点，若
∠BAD＝105°，则∠DCE的大小是
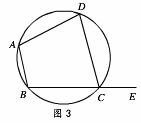
∠BAD＝105°，则∠DCE的大小是
| A．115° | B．l05° | C．100° | D．95° |
B
根据圆内接四边形的对角互补得到∠BAD+∠BCD=180°，而∠BCD与∠DEC为邻补角，得到∠DCE=∠BAD=105°．
解：∵四边形ABCD是圆内接四边形，
∴∠BAD+∠BCD=180°，
而∠BCD+∠DCE=180°，
∴∠DCE=∠BAD，
而∠BAD=105°，
∴∠DCE=105°．
故选B．
本题考查了圆内接四边形的性质：圆内接四边形的对角互补．也考查了邻补角的定义以及等角的补角相等．
解：∵四边形ABCD是圆内接四边形，
∴∠BAD+∠BCD=180°，
而∠BCD+∠DCE=180°，
∴∠DCE=∠BAD，
而∠BAD=105°，
∴∠DCE=105°．
故选B．
本题考查了圆内接四边形的性质：圆内接四边形的对角互补．也考查了邻补角的定义以及等角的补角相等．
练习册系列答案
阳光课堂课时优化作业系列答案
相关题目
中，
，
，求
的长度．
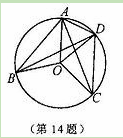
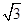，则顶点A运动到点A″的位置时，点A两次运动所经过的路程________（计算结果不取近似值）
