题目内容
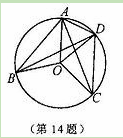
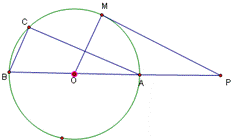
解：∵圆心角的度数和它们对的弧的度数相等，
∴
的度数等于84°，即∠COD=84°；
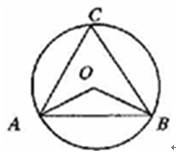
在△COD中，OC=OD（⊙O的半径），
∴∠OCD=∠ODC（等边对等角）；
又∵∠COD+∠OCD+∠ODC=180°，
∴∠OCD=48°；
而CA是∠OCD的平分线，
∴∠OCA=∠ACD，
∴∠OCA=∠ACD=24°；
在△AOC中，OA=OC（⊙O的半径），
∴∠CAO=∠OCA（等边对等角）；
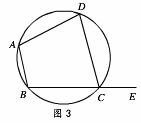
∵∠ABD=1/2∠AOD（同弧所对的圆周角是所对的圆心角的一半），
∠DCA=1/2∠AOD（同弧所对的圆周角是所对的圆心角的一半），
∴∠ABD=∠CAD，
∴∠ABD+∠CAO=48°；
故答案为：48°．
∴
的度数等于84°，即∠COD=84°；在△COD中，OC=OD（⊙O的半径），
∴∠OCD=∠ODC（等边对等角）；
又∵∠COD+∠OCD+∠ODC=180°，
∴∠OCD=48°；
而CA是∠OCD的平分线，
∴∠OCA=∠ACD，
∴∠OCA=∠ACD=24°；
在△AOC中，OA=OC（⊙O的半径），
∴∠CAO=∠OCA（等边对等角）；
∵∠ABD=1/2∠AOD（同弧所对的圆周角是所对的圆心角的一半），
∠DCA=1/2∠AOD（同弧所对的圆周角是所对的圆心角的一半），
∴∠ABD=∠CAD，
∴∠ABD+∠CAO=48°；
故答案为：48°．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
