题目内容
【题目】我们规定:一个多边形上任意两点间距离的最大值称为该多边形的“直径”.现有两个全等的三角形,边长分别为4、4、![]() .将这两个三角形相等的边重合拼成对角线互相垂直的凸四边形,那么这个凸四边形的“直径”为______.
.将这两个三角形相等的边重合拼成对角线互相垂直的凸四边形,那么这个凸四边形的“直径”为______.
【答案】6或3![]()
【解析】
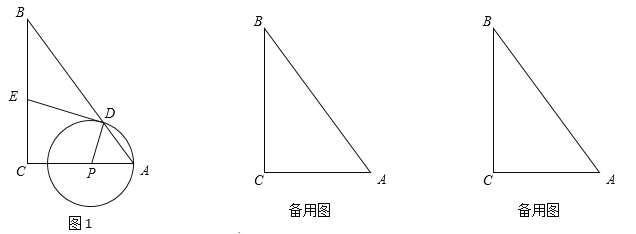
①如图1,由题意得,AB=AC=BD=CD=4,![]() 求得四边形ABDC是菱形,根据菱形的性质得到AD⊥BC,
求得四边形ABDC是菱形,根据菱形的性质得到AD⊥BC,![]() AO=OD,根据勾股定理得到
AO=OD,根据勾股定理得到![]()
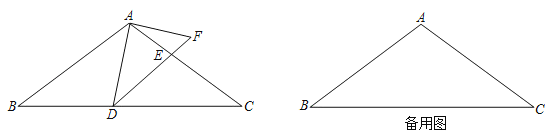
②如图2,由题意得,AB=AC=AD=4,![]() 得到AC垂直平分BD,求得AC⊥BD,BO=DO,设AO=x,则CO=4-x,根据勾股定理得到
得到AC垂直平分BD,求得AC⊥BD,BO=DO,设AO=x,则CO=4-x,根据勾股定理得到![]() 于是得到结论.
于是得到结论.
解:①如图1,由题意得,AB=AC=BD=CD=4,![]()
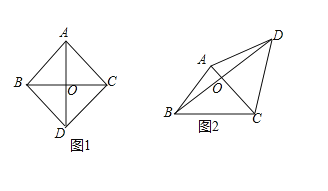
∴四边形ABDC是菱形,
∴AD⊥BC,![]() AO=OD,
AO=OD,
∴![]()
∴AD=6>![]() =BC,
=BC,
∴这个凸四边形的“直径”为6;
②如图2,由题意得,AB=AC=AD=4,![]()
∴AC垂直平分BD,
∴AC⊥BD,BO=DO,
设AO=x,则CO=4-x,
由勾股定理得,AB2-AO2=BC2-CO2,
![]()
解得:x=![]() ,
,
∴AO=![]() ,
,
∴![]()
∴BD=2BO=![]() ,
,
∵BD=![]() >4=AC,
>4=AC,
∴这个凸四边形的“直径”为![]() ,
,
综上所述:这个凸四边形的“直径”为6或![]() ,
,
故答案为6或![]()
.

 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案【题目】为了让学生掌握知识更加牢固,某校九年级物理组老师们将物理实验的教学方式由之前的理论教学改进为理论+实践,一段时间后,从九年级随机抽取15名学生,对他们在教学方式改进前后的物理实验成绩(百分制)进行整理、描述和分析(成绩用![]() 表示,共分成4组:A.
表示,共分成4组:A.![]() ,B.
,B.![]() ,C.
,C.![]() ,D.
,D.![]() ),下面给出部分信息:
),下面给出部分信息:
教学方式改进前抽取的学生的成绩在![]() 组中的数据为:80,83,85,87,89.
组中的数据为:80,83,85,87,89.
教学方式改进后抽取的学生成绩为:72,70,76,100,98,100,82,86,95,90,100,86,84,93,88.
教学方式改进前抽取的学生成绩频数分布直方图
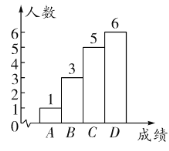
教学方式改进前后抽取的学生成绩对比统计表
统计量 | 改进前 | 改进后 |
平均数 | 88 | 88 |
中位数 |
|
|
众数 | 98 |
|
根据以上信息,解答下列问题:
(1)直接写出上述图表中![]() 的值;
的值;
(2)根据以上数据,你认为该校九年级学生的物理实验成绩在教学方式改进前好,还是改进后好?请说明理由(一条理由即可);
(3)若该校九年级有300名学生,规定物理实验成绩在90分及以上为优秀,估计教学方式改进后成绩为优秀的学生人数是多少?