Question

【题目】（1）如图，已知点 A（﹣4，4），一个以 A 为顶点的 45°角绕点 A 旋转，角 的两边分别交 x 轴正半轴，y 轴负半轴于 E、F，连接 EF．当△AEF 是直角三角形 时，点 E 的坐标是_________

（2）已知实数 x+y=12，则的最小值是_____

Answer 1

【答案】（8，0）或（4，0）.

【解析】

（1）

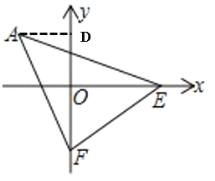
作AD垂直于y轴于点D，如图所示：

当∠AFE=90°

∴∠AFD+∠OFE=90°

∵∠OEF+∠OFE=90°

∴∠AFD=∠OEF

∵∠AFE=90°，∠EAF=45°

∴∠AEF=45°=∠EAF

∴AF=EF

在三角形ADF与三角形FOE中

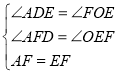
∴△ADF≌△FOE (AAS)

∴FO=AD=4,OE=DF=OD+FO=8

∴E（8，0）

当∠AEF=90°时，同理可得：OF=8，OE=4，∴E（4，0）

综上：E点的坐标为（8，0）或（4，0）.

（2）∵

∴

把代入得：

即

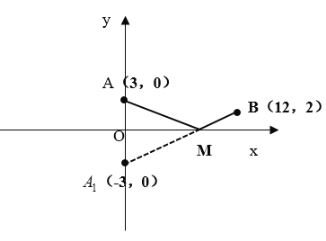
由两点距离公式可知，上式表示点M（x，0）到点A（0，3）与B（12，2）距离和.如图所示，找到A的对称点,即最小值为的距离，则=