Question

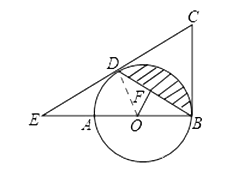
【题目】（本小题12分）如图，AB是⊙O的直径，BC为⊙O的切线，D为⊙O上的一点，CD=CB，延长CD交BA的延长线于点E．

（1）求证：CD为⊙O的切线；

（2）求证：∠C=2∠DBE．

（3）若EA=AO=2，求图中阴影部分的面积．（结果保留π）

Answer 1

【答案】（1）详见解析；（2）．

【解析】

试题（1）连接OD，由BC是⊙O的切线，可得∠ABC=90°，由CD=CB，OB=OD，易证得∠ODC=∠ABC=90°，即可证得CD为⊙O的切线．（2）在Rt△OBF中，∠ABD=30°，OF=1，可求得BD的长，∠BOD的度数，又由，即可求得答案．

试题解析：证明：连接OD，

∵BC是⊙O的切线，∴∠ABC=90°，

∵CD=CB， ∴∠CBD=∠CDB，

∵OB=OD，∴∠OBD=∠ODB，

∴∠ODC=∠ABC=90°，即OD⊥CD，

∵点D在⊙O上， ∴CD为⊙O的切线．

（2）如图，∠DOE=∠ODB+∠OBD=2∠DBE，

由（1）得：OD⊥EC于点D，∴∠E+∠C=∠E+∠DOE＝90°,

∴∠C=∠DOE＝2∠DBE．

（3）作OF⊥DB于点F,连接AD，

由EA=AO可得：AD是Rt△ODE斜边的中线，

∴AD=AO=OD,∴∠DOA=60°，∴∠OBD=30°，

又∵OB=AO=2，OF⊥BD，∴ OF=1，BF=，

∴BD=2BF=2，∠BOD=180°-∠DOA =120°，

∴．