��Ŀ����
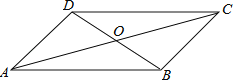
����Ŀ����ͼ����ʾ��һ����Ϊ2m����Ϊ2n�ij����Σ���ͼ�������ü������ֳ��ĸ�С�����Σ�Ȼ��ͼ�ڵķ�ʽƴ��һ�������Ρ�
(1)����Ϊͼ������Ӱ���ֵ������εı߳�����________��
(2)�������ֲ�ͬ�ķ����д���ʽ��ʾͼ������Ӱ���ֵ������
������___________________________________��
������___________________________________��
(3)�۲�ͼ�ڣ���д��![]() ��
��![]() ��
��![]() ����������ʽ֮��ĵ�����ϵ ��
����������ʽ֮��ĵ�����ϵ ��
(4)����(3)���еĵ�����ϵ������������⣺��![]() ��
��![]() ������
������![]() ��ֵ��
��ֵ��

���𰸡���1��mn����2���٣�(mn)2;��(m+n)24mn����3��(mn)2=(m+n)24mn����4��17.
��������
ƽ���ֳɺ�ÿ��С�����εij�Ϊm����Ϊn��
��1�������εı߳�=С�����εij�-����
��2����һ�ַ���Ϊ�������������-4��С������������ڶ��ֱ�ʾ����Ϊ����Ӱ����ΪС�����ε������
��3�����ã�m+n��2-4mn=��m-n��2����⣻
��4�����ã�a-b��2=��a+b��2-4ab����⣮
(1)��Ӱ���ֵ������εı߳�����mn��
(2)ͼ������Ӱ���ֵ����,
�����٣�(mn)2;����
�ڣ�(m+n)24mn��
(3)��������ʽ֮��ĵ�����ϵ��(mn)2=(m+n)24mn��
(4)��(3)��֪��(ab)2=(a+b)24ab��
��a+b=5,ab=2ʱ,ԭʽ=524��2=17.