题目内容
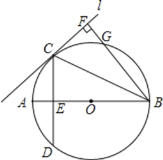
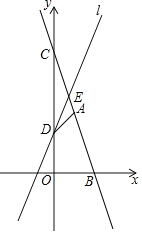
【题目】如图，过点A（1，3）的一次函数y＝kx+6（k≠0）的图象分别与x轴，y轴相交于B，C两点．
（1）求k的值；
（2）直线l与y轴相交于点D（0，2），与线段BC相交于点E．
（i）若直线l把△BOC分成面积比为1：2的两部分，求直线l的函数表达式；
（ⅱ）连接AD，若△ADE是以AE为腰的等腰三角形，求满足条件的点E的坐标．
【答案】（1）-3；（2）（i）y＝±x+2；（ⅱ）点E的坐标为：（
，
）或（
，）．
【解析】
（1）将点A的坐标代入一次函数y＝kx+6中，即可解得k的值；
（2）（i）先求出△BCO的面积，根据直线l把△BOC分成面积比为1：2的两部得出△CDE的面积，根据三角形面积公式得出E的横坐标，将横坐标代入y＝kx+6即可得到E的坐标，点E的坐标代入直线l表达式，即可求出直线l表达式；
（ⅱ）设点E（m，﹣3m+6），根据两点间的距离公式列出方程，解得点E的坐标．
（1）将点A的坐标代入一次函数y＝kx+6并解得：
k＝﹣3；
（2）一次函数y＝﹣3x+6分别与x轴，y轴相交于B，C两点，
则点B、C的坐标分别为：（2，0）、（0，6）；
（i）S△BCO＝
OB×CO＝2×6＝6，
直线l把△BOC分成面积比为1：2的两部分，
则S△CDE＝2或4，
而S△CDE＝
×CD×
＝4×＝2或4，
则＝1或2，
故点E（1，3）或（2，0），
将点E的坐标代入直线l表达式并解得：
直线l的表达式为：y＝±x+2；
（ⅱ）设点E（m，﹣3m+6），而点A、D的坐标分别为：（1，3）、（0，2），
则AE2＝（m﹣1）2+（3﹣3m）2，AD2＝2，ED2＝m2+（4﹣3m）2，
当AE＝AD时，（m﹣1）2+（3﹣3m）2＝2，解得：m＝（不合题意值已舍去）；
当AE＝ED时，同理可得：m＝；
综上，点E的坐标为：（，）或（，）．
