题目内容
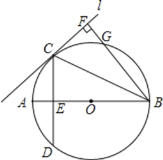
【题目】如图所示,已知AB是![]() 的直径,直线L与
的直径,直线L与![]() 相切于点C,
相切于点C,![]() ,CD交AB于E,
,CD交AB于E,![]() 直线L,垂足为F,BF交
直线L,垂足为F,BF交![]() 于C.
于C.
![]() 图中哪条线段与AE相等?试证明你的结论;
图中哪条线段与AE相等?试证明你的结论;
![]() 若
若![]() ,
,![]() ,求AB的值.
,求AB的值.
【答案】(1)见解析;(2)20.
【解析】
(1)观察图象知:只有FG的长度与AE相当,可猜想AE=FG,然后着手证明它们相等;求简单的线段相等,通常是证线段所在的三角形全等,那么本题需要构造全等三角形,连接AC、CG,然后证△AEC≌△GCF;连接BD,由于弧AC=弧AD,那么BA⊥CD,根据垂径定理知∠D=∠BCE;由弦切角定理知∠FCB=∠D=∠DCB,那么它们的余角也相等,即∠FBC=∠EBC,那么弧CG=弧AC,即AC=CG,再由角平分线的性质得CF=CE,根据HL即可判定所求的两个三角形全等,由此得证.
(2)由弦切角定理知∠FCG=∠FBC,它们的正弦值也相等,即可在Rt△FCG中,求得CG的长,也就得到了AC的长,在Rt△ACB中,CE⊥AB,由射影定理即可得到AB的长.
解:(1)FG=AE,理由如下:
连接CG、AC、BD;
∵![]() ,
,
∴BA⊥CD,
∴![]() ,即∠D=∠BCD;
,即∠D=∠BCD;
∵直线L切⊙O于C,
∴∠BCF=∠D=∠BCD,
∴∠FBC=∠ABC,
∴![]() ,CE=CF;
,CE=CF;
∴AC=CG;
△ACE和△GCF中,AC=CG、CE=CF,∠AEC=∠CFG=90°,
∴Rt△AEC≌Rt△GCF,则AE=FG.
(2)∵FC切⊙O于C,
∴∠FCG=∠FBC,即sin∠FCG=sin∠CBF=![]() ;
;
在Rt△FCG中,FG=AE=4,CG=FG÷sin∠FCG=4![]() ;
;
∴AC=CG=4![]() ;
;
在Rt△ABC中,CE⊥AB,由射影定理得:
AC2=AEAB,即AB=AC2÷AE=20.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目