题目内容
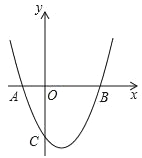
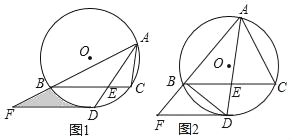
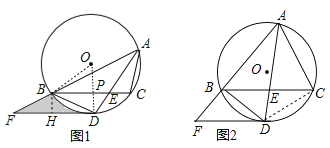
【题目】如图1,△ABC内接于⊙O,∠BAC的平分线交⊙O于点D,交BC于点E(BE>EC),且BD=2![]() .过点D作DF∥BC,交AB的延长线于点F.
.过点D作DF∥BC,交AB的延长线于点F.
(1)求证:DF为⊙O的切线;
(2)若∠BAC=60°,DE=![]() ,求图中阴影部分的面积;
,求图中阴影部分的面积;
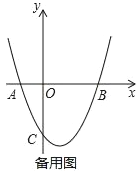
(3)若![]() ,DF+BF=8,如图2,求BF的长.
,DF+BF=8,如图2,求BF的长.
【答案】(1)证明见解析(2)9![]() ﹣2π;(3)3
﹣2π;(3)3
【解析】试题分析:(1)连结OD,如图1,由已知得到∠BAD=∠CAD,得到![]() ,再由垂径定理得OD⊥BC,由于BC∥EF,则OD⊥DF,于是可得结论;
,再由垂径定理得OD⊥BC,由于BC∥EF,则OD⊥DF,于是可得结论;
(2)连结OB,OD交BC于P,作BH⊥DF于H,如图1,先证明△OBD为等边三角形得到∠ODB=60°,OB=BD=![]() ,得到∠BDF=∠DBP=30°,在Rt△DBP中得到PD=
,得到∠BDF=∠DBP=30°,在Rt△DBP中得到PD=![]() ,PB=3,在Rt△DEP中利用勾股定理可算出PE=2,由于OP⊥BC,则BP=CP=3,得到CE=1,由△BDE∽△ACE,得到AE的长,再证明△ABE∽△AFD,可得DF=12,最后利用S阴影部分=S△BDF﹣S弓形BD=S△BDF﹣(S扇形BOD﹣S△BOD)进行计算;
,PB=3,在Rt△DEP中利用勾股定理可算出PE=2,由于OP⊥BC,则BP=CP=3,得到CE=1,由△BDE∽△ACE,得到AE的长,再证明△ABE∽△AFD,可得DF=12,最后利用S阴影部分=S△BDF﹣S弓形BD=S△BDF﹣(S扇形BOD﹣S△BOD)进行计算;
(3)连结CD,如图2,由![]() 可设AB=4x,AC=3x,设BF=y,由
可设AB=4x,AC=3x,设BF=y,由![]() 得到CD=BD=
得到CD=BD=![]() ,由△BFD∽△CDA,得到xy=4,再由△FDB∽△FAD,得到16﹣4y=xy,则16﹣4y=4,然后解方程即可得到BF=3.
,由△BFD∽△CDA,得到xy=4,再由△FDB∽△FAD,得到16﹣4y=xy,则16﹣4y=4,然后解方程即可得到BF=3.
试题解析:(1)连结OD,如图1,∵AD平分∠BAC交⊙O于D,∴∠BAD=∠CAD,∴![]() ,∴OD⊥BC,∵BC∥EF,∴OD⊥DF,∴DF为⊙O的切线;
,∴OD⊥BC,∵BC∥EF,∴OD⊥DF,∴DF为⊙O的切线;
(2)连结OB,连结OD交BC于P,作BH⊥DF于H,如图1,∵∠BAC=60°,AD平分∠BAC,∴∠BAD=30°,∴∠BOD=2∠BAD=60°,∴△OBD为等边三角形,∴∠ODB=60°,OB=BD=![]() ,∴∠BDF=30°,∵BC∥DF,∴∠DBP=30°,在Rt△DBP中,PD=
,∴∠BDF=30°,∵BC∥DF,∴∠DBP=30°,在Rt△DBP中,PD=![]() BD=
BD=![]() ,PB=
,PB=![]() PD=3,在Rt△DEP中,∵PD=
PD=3,在Rt△DEP中,∵PD=![]() ,DE=
,DE=![]() ,∴PE=
,∴PE=![]() =2,∵OP⊥BC,∴BP=CP=3,∴CE=3﹣2=1,易证得△BDE∽△ACE,∴AE:BE=CE:DE,即AE:5=1:
=2,∵OP⊥BC,∴BP=CP=3,∴CE=3﹣2=1,易证得△BDE∽△ACE,∴AE:BE=CE:DE,即AE:5=1: ![]() ,∴AE=
,∴AE=![]() ,∵BE∥DF,∴△ABE∽△AFD,∴
,∵BE∥DF,∴△ABE∽△AFD,∴![]() ,即
,即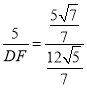 ,解得DF=12,在Rt△BDH中,BH=
,解得DF=12,在Rt△BDH中,BH=![]() BD=
BD=![]() ,∴S阴影部分=S△BDF﹣S弓形BD=S△BDF﹣(S扇形BOD﹣S△BOD)=
,∴S阴影部分=S△BDF﹣S弓形BD=S△BDF﹣(S扇形BOD﹣S△BOD)=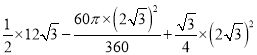 =
=![]() ;
;
(3)连结CD,如图2,由![]() 可设AB=4x,AC=3x,设BF=y,∵
可设AB=4x,AC=3x,设BF=y,∵![]() ,∴CD=BD=
,∴CD=BD=![]() ,∵∠F=∠ABC=∠ADC,∵∠FDB=∠DBC=∠DAC,∴△BFD∽△CDA,∴
,∵∠F=∠ABC=∠ADC,∵∠FDB=∠DBC=∠DAC,∴△BFD∽△CDA,∴![]() ,即
,即![]() ,∴xy=4,∵∠FDB=∠DBC=∠DAC=∠FAD,而∠DFB=∠AFD,∴△FDB∽△FAD,∴
,∴xy=4,∵∠FDB=∠DBC=∠DAC=∠FAD,而∠DFB=∠AFD,∴△FDB∽△FAD,∴![]() ,即
,即![]() ,整理得16﹣4y=xy,∴16﹣4y=4,解得y=3,即BF的长为3.
,整理得16﹣4y=xy,∴16﹣4y=4,解得y=3,即BF的长为3.

 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案【题目】立定跳远是体育中考选考项目之一,体育课上老师记录了某同学的一组立定跳远成绩如表:
成绩(m) | 2.3 | 2.4 | 2.5 | 2.4 | 2.4 |
则下列关于这组数据的说法,正确的是( )
A.众数是2.3B.平均数是2.4
C.中位数是2.5D.方差是0.01