题目内容
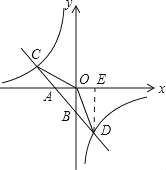
【题目】如图,已知一次函数y1=k1x+b的图象与x轴、y轴分别交于A、B两点,与反比例函数![]() 的图象分别交于C、D两点,点D(2,﹣3),点B是线段AD的中点.
的图象分别交于C、D两点,点D(2,﹣3),点B是线段AD的中点.
(1)求一次函数y1=k1x+b与反比例函数![]() 的解析式;
的解析式;
(2)求△COD的面积;
(3)直接写出y1>y2时自变量x的取值范围.

【答案】(1)y1=﹣![]() x﹣
x﹣![]() ,y2=-
,y2=-![]() (2)
(2)![]() (3)当x<﹣4或0<x<2时,y1>y2
(3)当x<﹣4或0<x<2时,y1>y2
【解析】
试题分析:(1)把点D的坐标代入y2=![]() 利用待定系数法即可求得反比例函数的解析式,作DE⊥x轴于E,根据题意求得A的坐标,然后利用待定系数法求得一次函数的解析式;
利用待定系数法即可求得反比例函数的解析式,作DE⊥x轴于E,根据题意求得A的坐标,然后利用待定系数法求得一次函数的解析式;
(2)联立方程求得C的坐标,然后根据![]() 即可求得△COD的面积;
即可求得△COD的面积;
(3)根据图象即可求得.
试题解析:(1)∵点D(2,﹣3)在反比例函数y2=![]() 的图象上,
的图象上,
∴k2=2×(﹣3)=﹣6,
∴y2=-![]() ;
;
作DE⊥x轴于E,
∵D(2,﹣3),点B是线段AD的中点,
∴A(﹣2,0),
∵A(﹣2,0),D(2,﹣3)在y1=k1x+b的图象上,
∴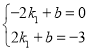 ,
,
解得k1=﹣![]() ,b=﹣
,b=﹣![]() ,
,
∴y1=﹣![]() x﹣
x﹣![]() ;,
;,
(2)由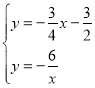 ,
,
解得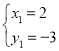 ,
,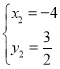 ,
,
∴C(﹣4,![]() ),
),
∴![]() =
=![]() ×
×![]() +
+![]() ×2×3=
×2×3=![]() ;
;
(3)当x<﹣4或0<x<2时,y1>y2.

练习册系列答案
相关题目
【题目】在“一日捐”活动中,九(2)班42名同学捐款金额统计如下表,则在这次活动中,该班同学捐款金额的众数是( )
金额(元) | 20 | 30 | 35 | 50 | 100 | 150 |
学生数(名) | 5 | 7 | 9 | 13 | 5 | 3 |
A.3B.35C.50D.150