��Ŀ����
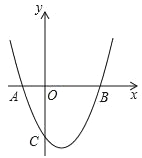
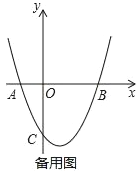
����Ŀ����ƽ��ֱ������ϵxOy�У�������y=x2+bx+c��x�ύ�ڵ�A��B��A��B����ࣩ�������ߵĶԳ���Ϊֱ��x=1��AB=4��
��1���������ߵı���ʽ��
��2����������������M��x1��y1����N��x2��y2������x1��1��x2��1��x1+x2��2�����ж�y1��y2�Ĵ�С����˵�����ɣ�
��3��ƽ�Ƹ������ߣ�ʹƽ�ƺ�������߾�����O������x�ύ�ڵ�D����ƽ�ƺ�������߶���Ϊ��P
������ODP�ǵ���ֱ�������Σ����P�����ꣻ
���ڢٵ������£�ֱ��x=m��0��m��3���ֱ��߶�BP��BC�ڵ�E��F���ҡ�BEF���������BPC�����=2��3��ֱ��д��m��ֵ��
���𰸡���1��y=x2��2x��3����2��y1��y2����3��m��ֵΪ1��3��2![]() ��
��
����������������1���ȸ��������ߺ�x��Ľ��㼰�߶εij�����������ߵĽ���ʽ��
��2�����������ߵĽ���ʽ�жϳ���M��N�Ĵ��λ�ã��ٸ��ݵ�M��N�ĺ�����ķ�Χ�жϺ���ֵ�Ĵ�С���ɣ�
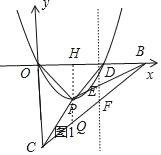
��3������PH��x����H�����ݵ��������ε����ʵõ�PH=OH=OD���������Ϊ������D��x����������ϣ�����D��x��ĸ������ϣ����P���������⼴�ɣ�
�ڵ���D��x����������ϣ��ӳ�HP��BC��Q�����ݴ���ϵ�������ֱ��BP�Ľ���ʽ��ֱ��BC�Ľ���ʽ��Ȼ�������BEF���������BPC�����=2��3�����m��ֵ������D��x��ĸ������ϣ��ӳ�HP��BC��Q��ͬ�����ֱ��BP�Ľ���ʽ��ͬ�����m��ֵ.
��⣺��1���������ߵĶԳ���Ϊֱ��x=1��AB=4��
��A����1��0����B��3��0����
�������߽���ʽΪy=��x+1����x��3����
��y=x2��2x��3��
��2��y1��y2���������£�
��x1��1��x2��1��
��M��N�ڶԳ�������࣬
��x1+x2��2��
��x2��1��1��x1��
���N��ֱ��x=1�ľ����M�㵽ֱ��x=1�ľ���Զ��
��y1��y2��
��3������PH��x����H��
�ߡ�OPDΪ����ֱ�������Σ�
��PH=OH=OD��
����D��x����������ϣ���ͼ1��
��P��m����m������D��2m��0����
�������ߵĽ���ʽΪy=x��x��2m����
��P��m����m�������m��m��2m��=��m�����m1=0����ȥ����m2=1����P��1����1����
����D��x��ĸ������ϣ���ͼ2��
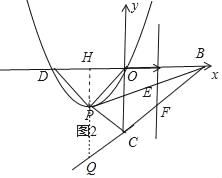
��P��m��m������D��2m��0����
�������ߵĽ���ʽΪy=x��x��2m����
��P��m��m�������m��m��2m��=m�����m1=0����ȥ����m2=��1����P����1����1����
����������P��������1����1����1����1����
�ڵ���D��x����������ϣ���ͼ1���ӳ�HP��BC��Q��
��ֱ��BP�Ľ���ʽΪy=px+q��
��B��3��0����P��1����1�������![]() �����
�����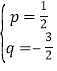 ��
��
��ֱ��BP�Ľ���ʽΪy=![]() x��
x��![]() ��
��
��ֱ��BC�Ľ���ʽΪy=x��3��
��Q��1����2����E��m��![]() m��
m��![]() ����F��m��m��3����
����F��m��m��3����
S��PBC=![]() ��1��3=
��1��3=![]() ��
��
�ߡ�BEF���������BPC�����=2��3��
��S��BEF=1��
��![]() ����
����![]() m+
m+![]() ����3��m��=1�����m1=5����ȥ����m2=1��
����3��m��=1�����m1=5����ȥ����m2=1��
����D��x��ĸ������ϣ���ͼ2���ӳ�HP��BC��Q��
ͬ���ɵ�ֱ��BP�Ľ���ʽΪy=![]() x��
x��![]() ��
��
��Q����1����4����E��m��![]() m��
m��![]() ����F��m��m��3����
����F��m��m��3����
S��PBC=![]() ��3��3=
��3��3=![]() ��
��
�ߡ�BEF���������BPC�����=2��3��
��S��BEF=3��
��![]() ����
����![]() m+
m+![]() ����3��m��=3�����m1=3+2
����3��m��=3�����m1=3+2![]() ����ȥ����m2=3��2
����ȥ����m2=3��2![]() ��
��
����������m��ֵΪ1��3��2![]() ��
��

 ��������ϵ�д�
��������ϵ�д�