题目内容
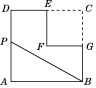
【题目】如图,在长方形ABCD中,AB=4,BC=7,点P是BC边上与点B不重合的动点,过点P的直线交CD的延长线于点R,交AD于点Q(点Q与点D不重合),且∠RPC=45°.设BP=x,梯形ABPQ的面积为y,求y与x之间的函数关系式,并求出自变量x的取值范围.
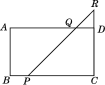
【答案】y=4x+8(0<x<3).
【解析】
由梯形面积公式S=![]() (AQ+BP)×AB,设BP=x,AB=4,需求得AQ,又∠RPC=45,AQ=AD-QD,QD=RD=RC-CD=PC-CD,由此得出y与x之间的函数关系;对于自变量x的取值范围,求临界条件Q与D重合时,BP=x=3,又Q与D不重合,故x<3.
(AQ+BP)×AB,设BP=x,AB=4,需求得AQ,又∠RPC=45,AQ=AD-QD,QD=RD=RC-CD=PC-CD,由此得出y与x之间的函数关系;对于自变量x的取值范围,求临界条件Q与D重合时,BP=x=3,又Q与D不重合,故x<3.
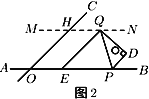
如图,过点D作DP′∥PQ,交BC于点P′,
则∠DP′C=∠RPC=45°,
∴P′C=CD=4,∴BP′=3.∴BP<3.
∵BP=x,∴PC=7-x.
在Rt△PCR中,∠C=90°,
∠RPC=45°,
∴CR=PC=7-x.
∴QD=RD=CR-CD
=7-x-4
=3-x,
∴AQ=AD-QD
=7-(3-x)
=4+x.
∴y=![]() (BP+AQ)·AB
(BP+AQ)·AB
=![]() (x+4+x)×4
(x+4+x)×4
=4x+8(0<x<3).

练习册系列答案
相关题目