题目内容
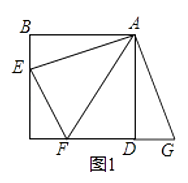
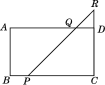
【题目】如图1,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,
,![]() .小明将一个含
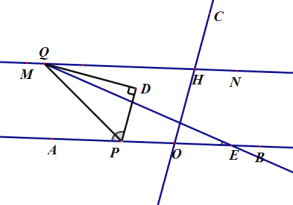
.小明将一个含![]() 的直角三角板
的直角三角板![]() 如图1所示放置,使顶点
如图1所示放置,使顶点![]() 落在直线
落在直线![]() 上,过点
上,过点![]() 作直线
作直线![]() 交直线
交直线![]() 于点
于点![]() (点
(点![]() 在
在![]() 左侧).
左侧).

(1)若![]() ,
,![]() ,则
,则![]() __________
__________![]() .
.
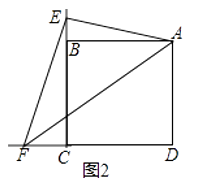
(2)若![]() 的角平分线交直线
的角平分线交直线![]() 于点
于点![]() ,如图2.
,如图2.
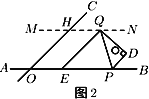

①当![]() ,
,![]() 时,求证:
时,求证:![]() .
.
②小明将三角板保持![]() 并向左平移,运动过程中,
并向左平移,运动过程中,![]() __________.(用
__________.(用![]() 表示).
表示).
【答案】(1)45;(2)①详见解析;②![]() 或
或![]() ;
;
【解析】
(1)根据平行线性质可得![]() ,再根据平行线性质得
,再根据平行线性质得![]() ;
;
(2)①根据平行线性质得![]() ,
,![]() ,结合角平分线定义可证
,结合角平分线定义可证![]() ,得
,得![]() ,根据平行线传递性可再证
,根据平行线传递性可再证![]() ;
;
②分两种情况当Q在H的右侧时,根据平行线性质可得∠BPD=∠BOC=α,∠MQP=∠QPB=60°+α,根据角平分线性质∠MQE=![]() (60°+α),故∠PEQ=∠MQE;当Q在H的右侧时,与上面同理,∠NQE=
(60°+α),故∠PEQ=∠MQE;当Q在H的右侧时,与上面同理,∠NQE=![]() (180°-60°-α),∠PEQ=∠NQE.
(180°-60°-α),∠PEQ=∠NQE.
(1)由![]() ,
,![]() ,可得
,可得![]() ,
,
而![]() ,则有
,则有![]() .
.
故![]()
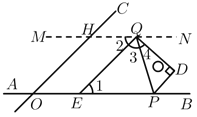
(2)
∵![]() ,
,![]() ,∴
,∴![]() ,
,
又∵![]() ,∴
,∴![]() ,
,
又∵![]() 平分
平分![]() ,∴
,∴![]() ,
,
又∵![]() ,∴
,∴![]() ,
,
且![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() .
.
②当Q在H的右侧时,
∵PD∥OC
∴∠BPD=∠BOC=α
∵MN∥AB
∴∠MQP=∠QPB=60°+α
又∵QE平分∠MQP
∴∠MQE=![]() (60°+α)=30°+
(60°+α)=30°+![]() α
α
∴∠PEQ=∠MQE=30°+![]() α
α
当Q在H的左侧时
∵PD∥OC
∴∠BPD=∠BOC=α
∵MN∥AB
∴∠NQP=180°-60°-α
又∵QE平分∠NQP
∠NQE=![]() (180°-60°-α)=60°-
(180°-60°-α)=60°-![]() α
α
∴∠PEQ=∠NQE=60°-![]() α
α
∴![]() 或
或![]() .
.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案【题目】某公司为了扩大经营,决定购进6台机器用于生产某活塞.现有甲、乙两种机器供选择,其中每种机器的价格和每台机器日生产活塞的数量如下表所示.经过预算,本次购买机器所耗资金不能超过34万元.
甲 | 乙 | |
价格(万元/台) | 7 | 5 |
每台日产量(个) | 100 | 60 |
(1)按该公司要求可以有几种购买方案?
(2)如果该公司购进的6台机器的日生产能力不能低于380个,那么为了节约资金应选择什么样的购买方案?