题目内容
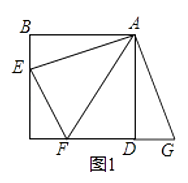
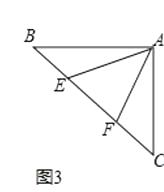
【题目】如图,点A是线段DE上一点,∠BAC=90°,AB=AC,BD⊥DE,CE⊥DE.
(1)求证:DE=BD+CE.
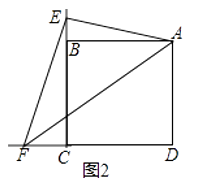
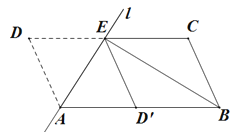
(2)如果是如图2这个图形,BD、CE、DE有什么数量关系?并证明.

【答案】(1)见解析;(2)BD=DE+CE,理由见解析.
【解析】
(1)先证△AEC≌△BDA得出AD=CE,BD=AE,从而得出DE=BD+CE;
(2)先证△ADB≌△CEA得出AD=CE,BD=AE,从而得出BD=DE+CE.
(1)∵BD⊥DE,CE⊥DE,∴∠D=∠E=90°,∴∠DBA+∠DAB=90°.
∵∠BAC=90°,∴∠DAB+∠CAE=90°,∴∠DBA=∠CAE.
∵AB=AC,∴△ADB≌△CEA,∴BD=AE,CE=AD,∴DE=AD+AE=CE+BD;
(2)BD=DE+CE.理由如下:
∵BD⊥DE,CE⊥DE,∴∠ADB=∠AEC=90°,∴∠ABD+∠BAD=90°.
∵∠BAC=90°,∴∠ABD+∠EAC=90°,∴∠BAD=∠EAC.
∵AB=AC,∴△ADB≌△CEA,∴BD=AE,CE=AD.
∵AE=AD+DE,∴BD=CE+DE.

练习册系列答案
相关题目