题目内容
如图,梯形ABCD中,AD∥BC,AB=CD,DE⊥BC于点E,且DE=1,AD=4,∠B=45°.
(1)直接写出BC的长;
(2)直线AB以每秒0.5个单位的速度向右平移,交AD于点P,交BC于点Q,则当直线AB的移动时间为多少秒,形成的四边形ABQP恰好为菱形?(结果精确到0.01秒);
(3)AB移动方向、速度如同第(2)题,移动时间为t秒,求经过t秒,AB扫过梯形ABCD的面 积S.(用含t的代数式表示,直接写出答案即可)
积S.(用含t的代数式表示,直接写出答案即可)
(1)直接写出BC的长;
(2)直线AB以每秒0.5个单位的速度向右平移,交AD于点P,交BC于点Q,则当直线AB的移动时间为多少秒,形成的四边形ABQP恰好为菱形?(结果精确到0.01秒);
(3)AB移动方向、速度如同第(2)题,移动时间为t秒,求经过t秒,AB扫过梯形ABCD的面
 积S.(用含t的代数式表示,直接写出答案即可)
积S.(用含t的代数式表示,直接写出答案即可)(1)AB=CD知∠B=∠C=45°,
∴EC=DE=1
∴BC=2CE+AD=2×1+4=6
(2)当四边形ABQP恰好为菱形时,
∴BQ=AB
∵AB=
DE=
∴移动时间为以
÷0.5≈1.414÷0.5≈2.83;
(3)当移动t秒时,PD=4-0.5t,QC=6-0.5t
∴s=S梯形ABCD-S梯形PQCD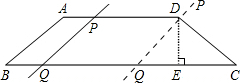
=
(4+6)×1-
(4-0.5t+6-0.5t)×1
=5-5+
t
=
t(0≤t≤8),
当8<t≤12时,s=S梯形ABCD-S△PQC,
=
(4+6)×1-
(6-0.5t)×1
=2+
t.
∴EC=DE=1
∴BC=2CE+AD=2×1+4=6
(2)当四边形ABQP恰好为菱形时,
∴BQ=AB
∵AB=
| 2 |
| 2 |
∴移动时间为以
| 2 |
(3)当移动t秒时,PD=4-0.5t,QC=6-0.5t
∴s=S梯形ABCD-S梯形PQCD

=
| 1 |
| 2 |
| 1 |
| 2 |
=5-5+
| 1 |
| 2 |
=
| 1 |
| 2 |
当8<t≤12时,s=S梯形ABCD-S△PQC,
=
| 1 |
| 2 |
| 1 |
| 2 |
=2+
| 1 |
| 4 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目




 (1)用t的代数式分别表示P、Q运动的路程;
(1)用t的代数式分别表示P、Q运动的路程;