Question

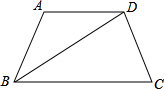
如图，在等腰梯形ABCD中，AB∥DC，AD=BC=5，DC=7，AB=13，点P从A点出发，以3个单位长度/秒的速度沿AD?DC向终点C运动，同时点Q从点B出发，以1个单位长度/秒的速度沿BA向点A运动，当有一点到达终点时，P、Q就同时停止运动．设运动的时间为t秒．
（1）用t的代数式分别表示P、Q运动的路程；
（2）求出梯形ABCD的面积；
（3）当t为多少秒时，四边形PQBC为平行四边形？

Answer 1

（1）P、Q运动的路程分别是3t、t；（2分）

（2）过点C作CE∥AD交AB于点E，过点C作CF⊥AB，垂足为F
在等腰梯形ABCD中，AB∥DC，AD=BC=5，DC=7，AB=13，
又CE∥AD
∴四边形AECD为平行四边形
∴CE=AD=BC=5，AE=CD=7
∴BE=AB-AE=13-7=6
在等腰△ECB中CF⊥AB，
∴F是BE的中点
∴EF=3
在Rt△CEF中CE=5，EF=3由勾股定理得
∴CF=4
∴梯形ABCD的面积=

(AB+CD)×CF

2

=

(13+7)×4

2

=40．（7分）

（3）当四边形PQBC为平行四边形时
PC=BQ即可
PC=5+7-3t，BQ=t
∴5+7-3t=t
∴t=3
当t=3秒时，四边形PQBC为平行四边形．（12分）