题目内容
【题目】如图1,对于平面上小于等于90°的∠MON,我们给出如下定义:若点P在∠MON的内部或边上,作PE⊥OM于点E,PF⊥ON于点F,则将PE+PF称为点P与∠MON的“点角距”,记作d(∠MON,P).如图2,在平面直角坐标系xOy中,x、y正半轴所组成的角为∠xOy.
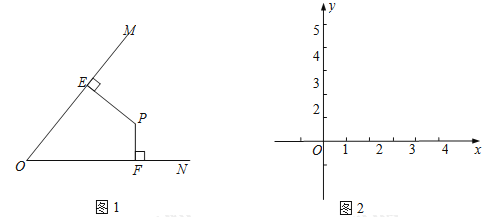
(1)已知点A(5,0)、点B(3,2),则d(∠xOy,A)= ,d(∠xOy,B)= .
(2)若点P为∠xOy内部或边上的动点,且满足d(∠xOy,P)=5,画出点P运动所形成的图形.
(3)如图3与图4,在平面直角坐标系xOy中,射线OT的函数关系式为y=![]() x(x≥0).
x(x≥0).
①在图3中,点C的坐标为(4,1),试求d(∠xOT,C)的值;
②在图4中,抛物线y=-![]() x2+2x+
x2+2x+![]() 经过A(5,0)与点D(3,4)两点,点Q是A,D两点之间的抛物线上的动点(点Q可与A,D两点重合),求当d(∠xOT,Q)取最大值时点Q 的坐标.
经过A(5,0)与点D(3,4)两点,点Q是A,D两点之间的抛物线上的动点(点Q可与A,D两点重合),求当d(∠xOT,Q)取最大值时点Q 的坐标.
【答案】(1)5,5;(2)点P运动所形成的图形是线段y=5-x(0≤x≤5).(3)![]() ;点Q的坐标为(4,
;点Q的坐标为(4,![]() ).
).
【解析】
试题分析:(1)首先根据点A(5,0)到x轴的距离是0,到y轴的距离是5,可得d(∠xOy,A)=0+5=5;然后根据点B(3,2)到x轴的距离是2,到y轴的距离是3,求出d(∠xOy,B)的值是多少即可.
(2)首先设点P的坐标是(x,y),然后根据d(∠xOy,P)=5,可得x+y=5,据此求出点P运动所形成的图形即可.
(3)①首先作CE⊥OT于点E,CF⊥x轴于点F,延长FC交OT于点H,则CF=1,然后设直线OT对应的函
数关系式为y=![]() x(x≥0),求出点H的坐标为H(4,
x(x≥0),求出点H的坐标为H(4,![]() ),进而求出CH,OH的值各是多少;最后根据相似三角形判定的方法,判断出△HEC∽△HFO,即可判断出
),进而求出CH,OH的值各是多少;最后根据相似三角形判定的方法,判断出△HEC∽△HFO,即可判断出![]() ,据此求出EC的值,即可求出d(∠xOT,C)的值是多少.
,据此求出EC的值,即可求出d(∠xOT,C)的值是多少.
②首先作QG⊥OT于点G,QH⊥x轴于点H,交OT于点K,设点Q的坐标为(m,n),其中3≤m≤5,则n
=-![]() m2+2m+
m2+2m+![]() ,然后判断出点K的坐标,以及HK,OK的大小,再判断出Rt△QGK∽Rt△OHK,即可判断出
,然后判断出点K的坐标,以及HK,OK的大小,再判断出Rt△QGK∽Rt△OHK,即可判断出![]() ,据此求出QG=
,据此求出QG=![]() ;最后求出d(∠xOT,Q)的值,根据二次函数最值的求法,求出当d(∠xOT,Q)取最大值时点Q 的坐标即可.
;最后求出d(∠xOT,Q)的值,根据二次函数最值的求法,求出当d(∠xOT,Q)取最大值时点Q 的坐标即可.
试题解析:(1)∵点A(5,0)到x轴的距离是0,到y轴的距离是5,
∴d(∠xOy,A)=0+5=5,
∵点B(3,2)到x轴的距离是2,到y轴的距离是3,
∴d(∠xOy,B)=2+3=5.
综上,可得d(∠xOy,A)=5,d(∠xOy,B)=5.
(2)设点P的坐标是(x,y),
∵d(∠xOy,P)=5,
∴x+y=5,
∴点P运动所形成的图形是线段y=5-x(0≤x≤5).
(3)①如图3,作CE⊥OT于点E,CF⊥x轴于点F,延长FC交OT于点H,则CF=1,
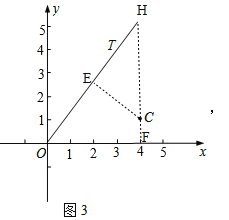
∵直线OT对应的函数关系式为y=![]() x(x≥0),
x(x≥0),
∴点H的坐标为H(4,![]() ),
),
∴CH=![]() 1=
1=![]() ,OH=
,OH=![]()
∵CE⊥OT,
∴∠OHF+∠HCE=90°,
又∵∠OHF+∠HOF=90°,
∴∠HCE=∠HOF,
在△HEC和△HFO中,
![]()
∴△HEC∽△HFO,
∴![]() ,
,
即 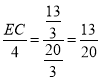
∴EC=![]() ,
,
∴d(∠xOT,C)=![]() +1=
+1=![]()
②如图4,作QG⊥OT于点G,QH⊥x轴于点H,交OT于点K,
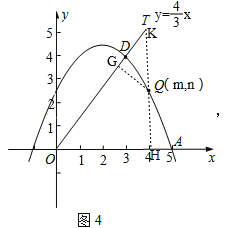
设点Q的坐标为(m,n),其中3≤m≤5,
则n=-![]() m2+2m+
m2+2m+![]() ,
,
∴点K的坐标为(m,![]() m),QK=
m),QK=![]() mn,
mn,
∴HK=![]() m,OK=
m,OK=![]() m.
m.
∵Rt△QGK∽Rt△OHK,
∴![]() ,
,
∴QG=![]() ,
,
∴d(∠xOT,Q)=QG+QH
=![]() +n
+n
=![]() m+
m+![]() n
n
=![]() m+
m+![]() (-
(-![]() m2+2m+
m2+2m+![]() )
)
=-![]() m2+
m2+![]() m+1
m+1
=![]() (m-4)2+
(m-4)2+![]()
∵3≤m≤5,
∴当m=4时,d(∠AOB,Q)取得最大值![]() .
.
此时,点Q的坐标为(4,![]() ).
).

【题目】某市居民使用自来水按如下标准收费(水费按月缴纳):
户月用水量 | 单价 |
不超过12 m3的部分 | a元∕m3 |
超过12 m3但不超过20 m3的部分 | 1.5a元∕m3 |
超过20 m3的部分 | 2a元∕m3 |
(1) 当a=2时,某用户一个月用了28 m3水,求该用户这个月应缴纳的水费;
(2) 设某户月用水量为n 立方米,当n>20时,则该用户应缴纳的水费_____________元(用含a、n的整式表示);
(3) 当a=2时,甲、乙两用户一个月共用水40 m3,已知甲用户缴纳的水费超过了24元,设甲用户这个月用水xm3,,试求甲、乙两用户一个月共缴纳的水费(用含x的整式表示).



