题目内容
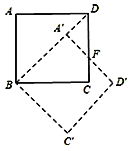
【题目】如图所示，正方形ABCD的边长等于2，它绕顶点B按顺时针方向旋转得到正方形A′BC′D′．在这个旋转过程中：
（1）旋转中心是什么？
（2）若旋转角为45°，边CD与A′D′交于F，求DF的长度．
【答案】（1）B点；（2）
．
【解析】试题分析：（1）由旋转中心定义可得.
(2)旋转45°后，可以得到点B、A′、D三点共线，且构造A’DF是等腰直角三角形,先求DA’,再求DF.
试题解析：
解：（1）旋转中心为B点；
（2）如图所示：∵旋转角为45°，
∴∠ABA′=45°．∵四边形ABCD为正方形，
∴∠ABD=45°，
∠A′DF=45°．
∴∠ABA′=∠ABD．
∴点B、A′、D三点在一条直线上．
在Rt△ABD中，BD=
．
∵A′D=BD﹣BA′，∴A′D=
．在Rt△A′DF中，
．
练习册系列答案
相关题目
